Acid-Base Properties of Solutions

14.3 Acid-Base Properties of Solutions

Learning Objectives

To understand the concept of conjugate acid–base pairs.
To know the relationship between acid or base strength and the magnitude of K_a, K_b, pK_a, and pK_b.
To understand the leveling effect.
To be able to calculate pH and pOH of aqueous solutions.
To recognize buffered solutions.

We now turn our attention to acid–base reactions to see how the concepts of chemical equilibrium and equilibrium constants can deepen our understanding of this kind of chemical behavior. We begin with a qualitative description of acid–base equilibriums in terms of the Brønsted-Lowry model. We then define the pH scale and then proceed to a discussion of buffered solutions.

Conjugate Acid–Base Pairs

In aqueous solutions, acids and bases can be defined in terms of the transfer of a proton from an acid to a base. Thus for every acidic species in an aqueous solution, there exists a species derived from the acid by the loss of a proton. These two species that differ by only a proton constitute a conjugate acid–base pairAn acid and a base that differ by only one hydrogen ion.. For example, in the reaction of HCl with water (Equation 14.3(eq1)), HCl, the parent acid, donates a proton to a water molecule, the parent base, thereby forming Cl⁻. Thus HCl and Cl⁻ constitute a conjugate acid–base pair. By convention, we always write a conjugate acid–base pair as the acid followed by its conjugate base. In the reverse reaction, the Cl⁻ ion in solution acts as a base to accept a proton from H₃O⁺, forming H₂O and HCl. Thus H₃O⁺ and H₂O constitute a second conjugate acid–base pair. In general, any acid–base reaction must contain two conjugate acid–base pairs, which in this case are HCl/Cl⁻ and H₃O⁺/H₂O.

Note the Pattern

All acid–base reactions contain two conjugate acid–base pairs.

Equation 14.3(eq1)

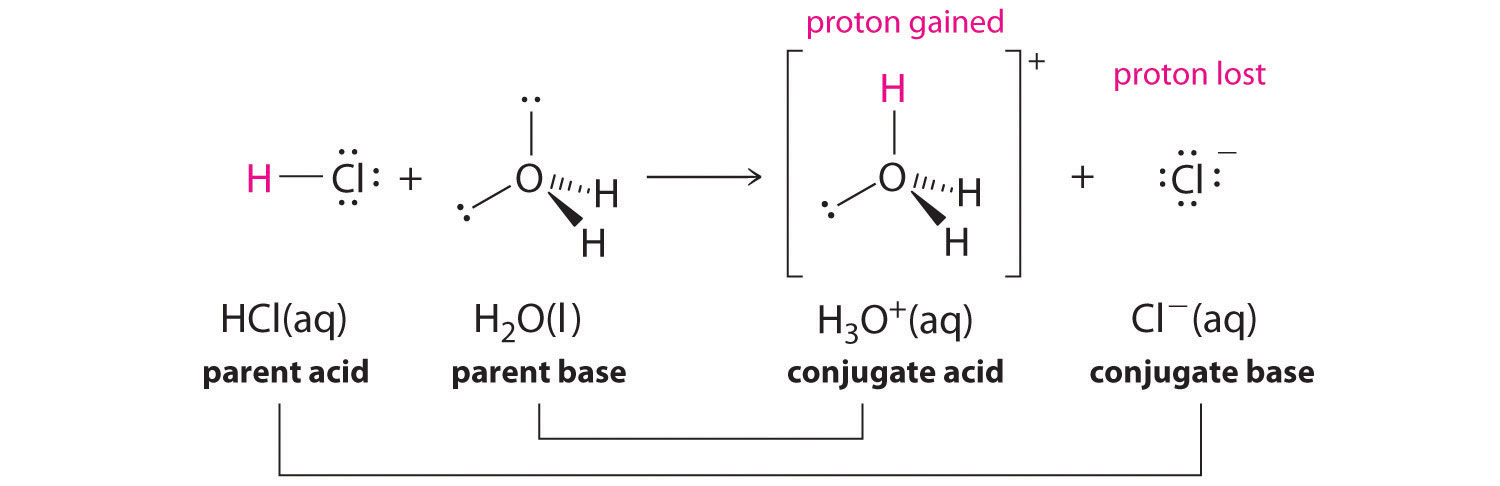
Similarly, in the reaction of acetic acid with water, acetic acid donates a proton to water, which acts as the base. In the reverse reaction, H₃O⁺ is the acid that donates a proton to the acetate ion, which acts as the base. Once again, we have two conjugate acid–base pairs: the parent acid and its conjugate base (CH₃CO₂H/CH₃CO₂⁻) and the parent base and its conjugate acid (H₃O⁺/H₂O).

Equation 14.3(eq2)

In the reaction of ammonia with water to give ammonium ions and hydroxide ions (Equation 14.3(eq3)), ammonia acts as a base by accepting a proton from a water molecule, which in this case means that water is acting as an acid. In the reverse reaction, an ammonium ion acts as an acid by donating a proton to a hydroxide ion, and the hydroxide ion acts as a base. The conjugate acid–base pairs for this reaction are NH₄⁺/NH₃ and H₂O/OH⁻. Some common conjugate acid–base pairs are shown in Figure 14.3(a).

Equation 14.3(eq3)

Figure 14.3(a) The Relative Strengths of Some Common Conjugate Acid–Base Pairs

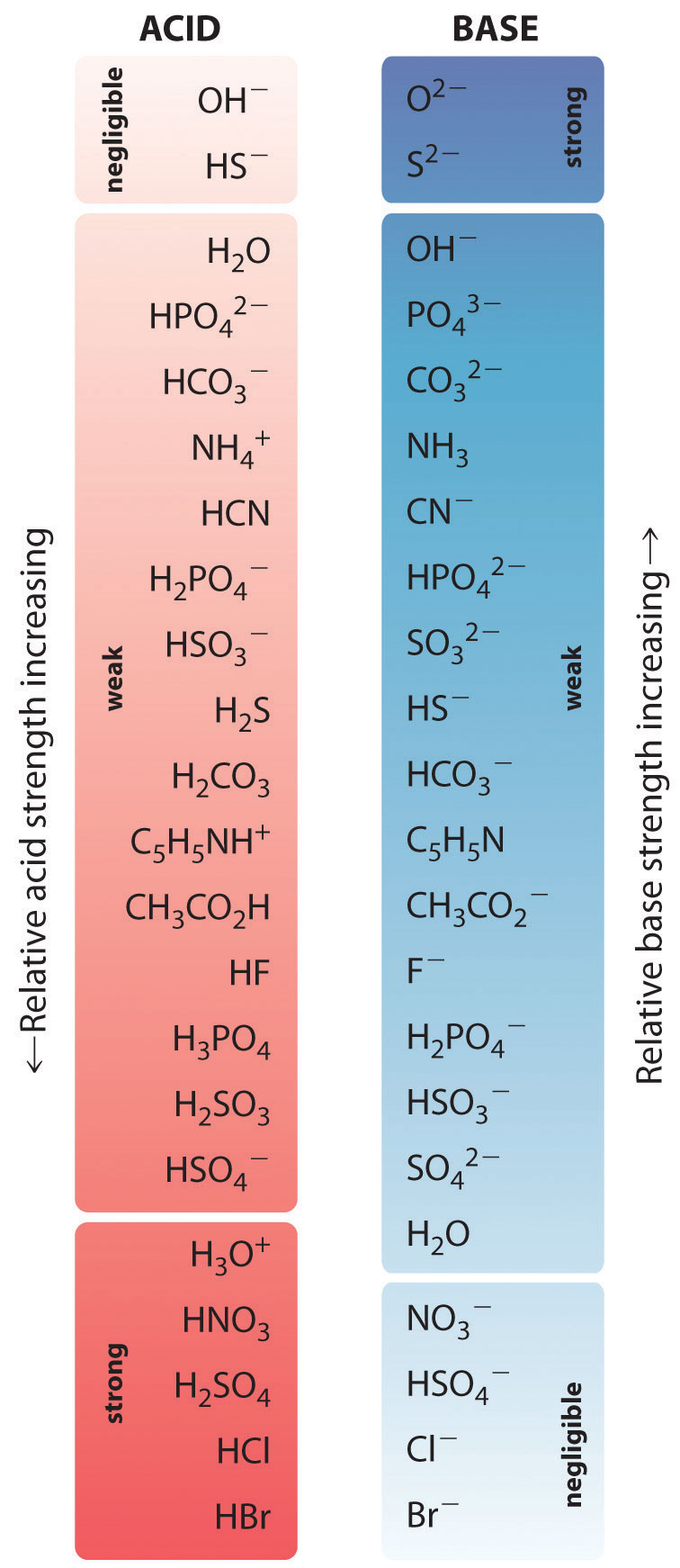
The strongest acids are at the bottom left, and the strongest bases are at the top right. The conjugate base of a strong acid is a very weak base, and, conversely, the conjugate acid of a strong base is a very weak acid.

Acid–Base Equilibrium Constants: K_a and pK_a

The magnitude of the equilibrium constant for an ionization reaction can be used to determine the relative strengths of acids and bases. For example, the general equation for the ionization of a weak acid in water, where HA is the parent acid and A⁻ is its conjugate base, is as follows:

Equation 14.3(eq4)

HA(aq) + H_{2} O(l) ⇌ H_{3} O^{+} (aq) + A^{-} (aq)

In this course, we are only concerned with the relative magnitudes (bigger or smaller) of equilibrium constants. In Elementary General Chemistry students will never be asked to calculate an equilibrium constant or perform algebraic manipulations to the equilibrium constant expression. However, for the purposes of understanding, we do need to define what this particular equilibrium constant represents. The equilibrium constant for this dissociation is as follows:

Equation 14.3(eq5)

K = \frac{[H_{3} O^{+}] [A^{-}]}{[H_{2} O] [HA]}

The square brackets around the formulas indicate molar concentration. The molar concentration of water, [H₂O], is essentially constant for all reactions in aqueous solution, so [H₂O] in Equation 14.3(eq5) can be incorporated into a new quantity, the acid ionization constant (K_a)An equilibrium constant for the ionization (dissociation) of a weak acid (HA) with water, $HA(aq)$ + $H_{2} O(l)$ ⇌ $H_{3} O(aq)$ + $A^{-} (aq),$ in which the concentration of water is treated as a constant: $K_{a}$ = $[H_{3} O^{+}] [A^{-}] / [HA] .$ , also called the acid dissociation constant:

Equation 14.3(eq6)

K_{a} = K [H_{2} O] = \frac{[H_{3} O^{+}] [A^{-}]}{[HA]}

Thus the numerical values of K and K_a differ by the concentration of water (55.3 M). Again, for simplicity, H₃O⁺ can be written as H⁺ in Equation 14.3(eq6). Keep in mind, though, that free H⁺ does not exist in aqueous solutions and that a proton is transferred to H₂O in all acid ionization reactions to form H₃O⁺. The larger the K_a, the stronger the acid and the higher the H⁺ concentration at equilibrium. Like all equilibrium constants, acid–base ionization constants are actually measured in terms of the activities of H⁺ or OH⁻, thus making them unitless. The values of K_a for a number of common acids are given in Table 14.3(1) .

Table 14.3(1) Values of K_a and pK_a for Selected Acids (HA) and Their Conjugate Bases (A⁻)

Acid	HA	K _a	pK_a
*The number in parentheses indicates the ionization step referred to for a polyprotic acid.
hydroiodic acid	HI	2 × 10⁹	−9.3
sulfuric acid (1)*	H₂SO₄	1 × 10²	−2.0
nitric acid	HNO₃	2.3 × 10¹	−1.37
hydronium ion	H₃O⁺	1.0	0.00
sulfuric acid (2)*	HSO₄⁻	1.0 × 10⁻²	1.99
hydrofluoric acid	HF	6.3 × 10⁻⁴	3.20
nitrous acid	HNO₂	5.6 × 10⁻⁴	3.25
formic acid	HCO₂H	1.78 × 10⁻⁴	3.750
benzoic acid	C₆H₅CO₂H	6.3 × 10⁻⁵	4.20
acetic acid	CH₃CO₂H	1.7 × 10⁻⁵	4.76
pyridinium ion	C₅H₅NH⁺	5.9 × 10⁻⁶	5.23
hypochlorous acid	HOCl	4.0 × 10⁻⁸	7.40
hydrocyanic acid	HCN	6.2 × 10⁻¹⁰	9.21
ammonium ion	NH₄⁺	5.6 × 10⁻¹⁰	9.25
water	H₂O	1.0 × 10⁻¹⁴	14.00
acetylene	C₂H₂	1 × 10⁻²⁶	26.0
ammonia	NH₃	1 × 10⁻³⁵	35.0

We can use negative logarithms to avoid exponential notation in writing acid and base ionization constants, by defining pK_a as follows:

Equation 14.3(eq7)

pK_a = −log₁₀K_a

Equation 14.3(eq8)

K_{a} = 10^{- p K_{a}}

Because of the use of negative logarithms, smaller values of pK_a correspond to larger acid ionization constants and hence stronger acids. For example, nitrous acid (HNO₂), with a pK_a of 3.25, is about a 1,000,000 times stronger acid than hydrocyanic acid (HCN), with a pK_a of 9.21.

The relative strengths of some common acids and their conjugate bases are shown graphically in Figure 14.3(a). The conjugate acid–base pairs are listed in order (from top to bottom) of increasing acid strength, which corresponds to decreasing values of pK_a. At the bottom left of Figure 14.3(a) are the common strong acids; at the top right are the most common strong bases. Notice the inverse relationship between the strength of the parent acid and the strength of the conjugate base. Thus the conjugate base of a strong acid is a very weak base, and the conjugate base of a very weak acid is a strong base.

Note the Pattern

The conjugate base of a strong acid is a weak base and vice versa.

Solutions of Strong Acids and Bases: The Leveling Effect

You will notice in Table 14.3(1) that acids like H₂SO₄ and HNO₃ lie above the hydronium ion, meaning that they have pK_a values less than zero and are stronger acids than the H₃O⁺ ion.The acidic proton in virtually all oxoacids is bonded to one of the oxygen atoms of the oxoanion. Thus nitric acid should properly be written as HONO₂. Unfortunately, however, the formulas of oxoacids are almost always written with hydrogen on the left and oxygen on the right, giving HNO₃ instead. In fact, all six of the common strong acids that we have already encountered have pK_a values less than zero, which means that they have a greater tendency to lose a proton than does the H₃O⁺ ion. Conversely, the conjugate bases of these strong acids are weaker bases than water. Consequently, the proton-transfer equilibriums for these strong acids lie far to the right, and adding any of the common strong acids to water results in an essentially stoichiometric reaction of the acid with water to form a solution of the H₃O⁺ ion and the conjugate base of the acid.

Although K_a for HI is about 10⁸ greater than K_a for HNO₃, the reaction of either HI or HNO₃ with water gives an essentially stoichiometric solution of H₃O⁺ and I⁻ or NO₃⁻. In fact, a 0.1 M aqueous solution of any strong acid actually contains 0.1 M H₃O⁺, regardless of the identity of the strong acid. This phenomenon is called the leveling effectThe phenomenon that makes $H_{3} O^{+}$ the strongest acid that can exist in water. Any species that is a stronger acid than $H_{3} O^{+}$ is leveled to the strength of $H_{3} O^{+}$ in aqueous solution.: any species that is a stronger acid than the conjugate acid of water (H₃O⁺) is leveled to the strength of H₃O⁺ in aqueous solution because H₃O⁺ is the strongest acid that can exist in equilibrium with water. Consequently, it is impossible to distinguish between the strengths of acids such as HI and HNO₃ in aqueous solution, and an alternative approach must be used to determine their relative acid strengths.

Note the Pattern

In aqueous solutions, [H₃O⁺] is the strongest acid and OH⁻ is the strongest base that can exist in equilibrium with H₂O.

The pH Scale

One of the key factors affecting reactions that occur in dilute solutions of acids and bases is the concentration of H⁺ and OH⁻ ions. The pH scaleA logarithmic scale used to express the hydrogen ion $(H^{+})$ concentration of a solution, making it possible to describe acidity or basicity quantitatively. provides a convenient way of expressing the hydrogen ion (H⁺) concentration of a solution and enables us to describe acidity or basicity in quantitative terms.

Pure liquid water contains extremely low but measurable concentrations of H₃O⁺(aq) and OH⁻(aq) ions produced via an autoionization reaction, in which water acts simultaneously as an acid and as a base:

Equation 14.3(eq9)

H₂O(l) + H₂O(l) ⇌ H₃O⁺(aq) + OH⁻(aq)

The concentration of hydrogen ions in pure water is only 1.0 × 10⁻⁷ M at 25°C. Because the autoionization reaction produces both a proton and a hydroxide ion, the OH⁻ concentration in pure water is also 1.0 × 10⁻⁷ M. Pure water is a neutral solutionA solution in which the total positive charge from all the cations is matched by an identical total negative charge from all the anions., in which [H⁺] = [OH⁻] = 1.0 × 10⁻⁷ M.

The pH scale describes the hydrogen ion concentration of a solution in a way that avoids the use of exponential notation; pHThe negative base-10 logarithm of the hydrogen ion concentration: $pH = - log [H^{+}] .$ is defined as the negative base-10 logarithm of the hydrogen ion concentration:pH is actually defined as the negative base-10 logarithm of hydrogen ion activity. As you will learn in a more advanced course, the activity of a substance in solution is related to its concentration. For dilute solutions such as those we are discussing, the activity and the concentration are approximately the same.

Equation 14.3(eq10)

pH = −log[H⁺]

Conversely,

Equation 14.3(eq11)

[H⁺] = 10^−pH

Because the hydrogen ion concentration is 1.0 × 10⁻⁷ M in pure water at 25°C, the pH of pure liquid water (and, by extension, of any neutral solution) is

Equation 14.3(eq12)

pH = −log[1.0 × 10⁻⁷] = 7.00

Adding an acid to pure water increases the hydrogen ion concentration and decreases the hydroxide ion concentration because a neutralization reaction occurs. Because the negative exponent of [H⁺] becomes smaller as [H⁺] increases, the pH decreases with increasing [H⁺]. For example, a 1.0 M solution of a strong monoprotic acid such as HCl or HNO₃ has a pH of 0.00:

Equation 14.3(eq13)

pH = −log[1.0] = 0.00

Be aware how the convention for significant figures is applied to pH's. The [H⁺] has as many significant figures as there are to the RIGHT of the decimal in the pH. So a pH=4 offers zero significant figures and only an order of magnitude for the [H⁺]. A pH of 4.000 offers three significant figures for the [H⁺]. Here are some more examples-

pH	[H⁺]
3	10^-3
3.0	1 × 10^-3
4.347	4.50 × 10^-5
4.8	2 × 10^-5

The last example in the table deserves a little explanation. A pH meter reading 4.8 is only providing the [H⁺] to one significant figure. If, however, you have prepared a solution that is known to be 2 × 10^-5 M and you were calculating the pH, you would get 4.7. The apparent contradiction is explained by remembering the last significant figure is always in doubt.

Note the Pattern

pH decreases with increasing [H⁺].

Conversely, adding a base to pure water increases the hydroxide ion concentration and decreases the hydrogen ion concentration. Because the autoionization reaction of water does not go to completion, neither does the neutralization reaction. Even a strongly basic solution contains a detectable amount of H⁺ ions. For example, a 1.0 M OH⁻ solution has [H⁺] = 1.0 × 10⁻¹⁴ M. The pH of a 1.0 M NaOH solution is therefore

Equation 14.3(eq14)

pH = −log[1.0 × 10⁻¹⁴] = 14.00

For practical purposes, the pH scale runs from pH = 0 (corresponding to 1 M H⁺) to pH 14 (corresponding to 1 M OH⁻), although pH values less than 0 or greater than 14 are possible.

We can summarize the relationships between acidity, basicity, and pH as follows:

If pH = 7.0, the solution is neutral.
If pH < 7.0, the solution is acidic.
If pH > 7.0, the solution is basic.

Keep in mind that the pH scale is logarithmic, so a change of 1.0 in the pH of a solution corresponds to a tenfold change in the hydrogen ion concentration. The foods and consumer products we encounter daily represent a wide range of pH values, as shown in Figure 14.3(b) .

Figure 14.3(b) A Plot of pH versus [H⁺] for Some Common Aqueous Solutions

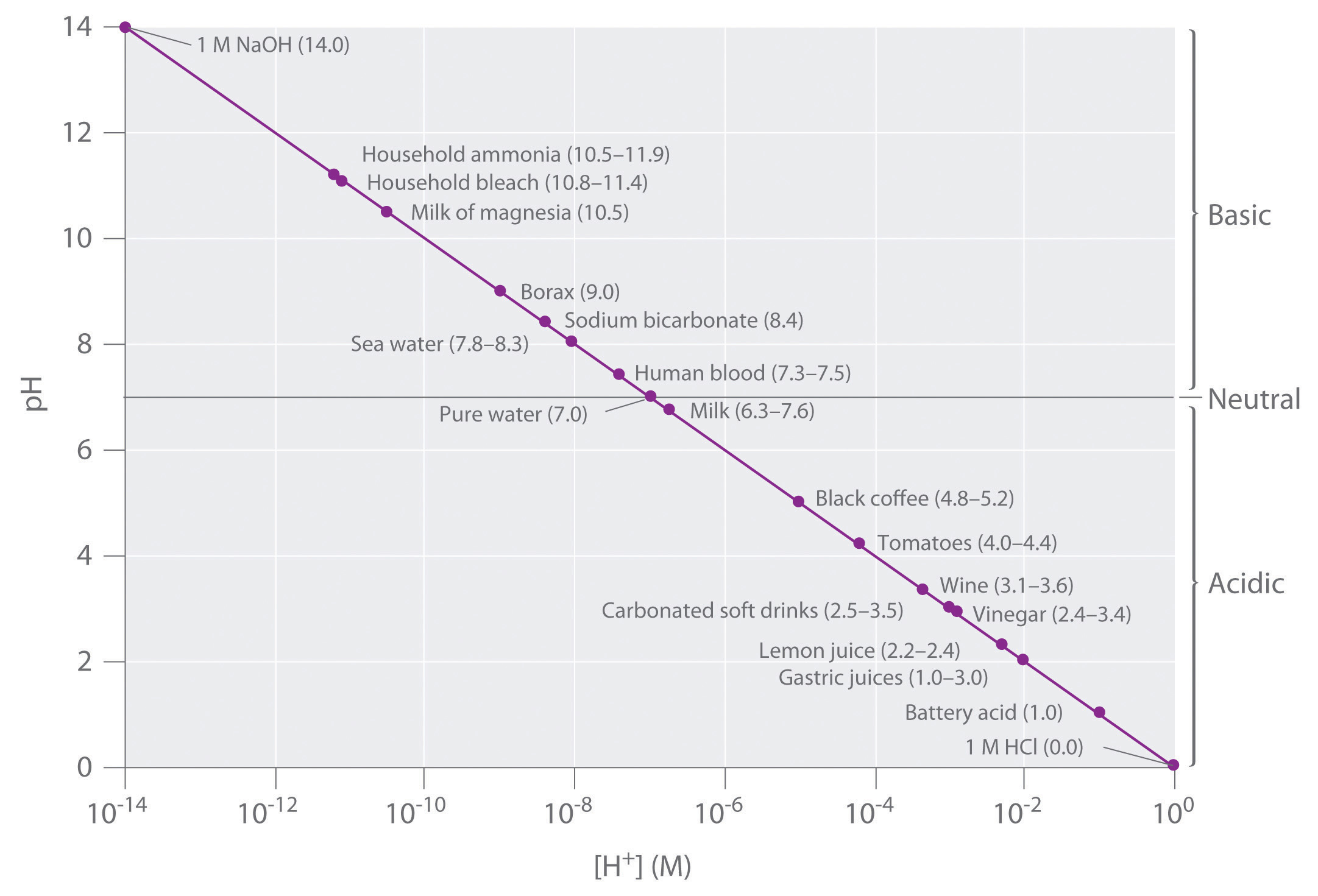
Although many substances exist in a range of pH values (indicated in parentheses), they are plotted using typical values.

Example 14.3-1

What is the pH of a 2.1 × 10⁻² M aqueous solution of HClO₄?
The pH of a vinegar sample is 3.80. What is its hydrogen ion concentration?

Given: molarity of acid or pH

Asked for: pH or [H⁺]

Strategy:

Using the balanced chemical equation for the acid dissociation reaction and Equation 14.3(eq11) or 14.3(eq10), determine [H⁺] and convert it to pH or vice versa.

Solution:

HClO₄ (perchloric acid) is a strong acid, so it dissociates completely into H⁺ ions and ClO₄⁻ ions:
HClO₄(l) → H⁺(aq) + ClO₄⁻(aq)
The H⁺ ion concentration is therefore the same as the perchloric acid concentration. The pH of the perchloric acid solution is thus
pH = −log[H⁺] = −log(2.1 × 10⁻²) = 1.68
The result makes sense: the H⁺ ion concentration is between 10⁻¹ M and 10⁻² M, so the pH must be between 1 and 2.

Note: The assumption that [H⁺] is the same as the concentration of the acid is valid for only strong acids. Because weak acids do not dissociate completely in aqueous solution, a more complex procedure is needed to calculate the pH of their solutions, which we will describe after we tackle equilibrium quantitatively.
We are given the pH and asked to calculate the hydrogen ion concentration. From Equation 14.3(eq10),
10^−pH = [H⁺]

Thus [H⁺] = 10^−3.80 = 1.6 × 10⁻⁴ M.

Exercise

What is the pH of a 3.0 × 10⁻⁵ M aqueous solution of HNO₃?
What is the hydrogen ion concentration of turnip juice, which has a pH of 5.41?

Answer:

pH = 4.52
[H⁺] = 3.9 × 10⁻⁶ M

Tools have been developed that make the measurement of pH simple and convenient (Figure 14.3(c)). For example, pH paper consists of strips of paper impregnated with one or more acid–base indicatorsAn intensely colored organic molecule whose color changes dramatically depending on the pH of the solution., which are intensely colored organic molecules whose colors change dramatically depending on the pH of the solution. Placing a drop of a solution on a strip of pH paper and comparing its color with standards give the solution’s approximate pH. A more accurate tool, the pH meter, uses a glass electrode, a device whose voltage depends on the H⁺ ion concentration.

Figure 14.3(c) Two Ways of Measuring the pH of a Solution: pH Paper and a pH Meter

Note that both show that the pH is between 1 and 2, but the pH meter gives a more precise value. Image Credit: Highland Community College, Freeport, IL.

Example 14.3-2

What are [H⁺] and [OH^-] for an aqueous solution whose pH is 4.88?

Solution

We need to evaluate the expression

[H⁺] = 10^-4.88

Depending on the calculator you use, the method for solving this problem will vary. In some cases, the "-4.88" is entered and a "10^x" key is pressed; for other calculators, the sequence of keystrokes is reversed. In any case, the correct numerical answer is as follows:

[H⁺] = 1.3 × 10^-5 M

Because 4.88 has two digits after the decimal point, [H⁺] is limited to two significant figures. From this, [OH^-] can be determined:

{[OH}^{-}] = \frac{1 \times 10^{- 14}}{1.3 \times 10^{- 5}} = 7.7 \times 10^{- 10} M

Test Yourself

What are [H⁺] and [OH^-] for an aqueous solution whose pH is 10.36?

Answer

[H⁺] = 4.4 × 10^-11 M; [OH^-] = 2.3 × 10^-4 M

There is an easier way to relate [H⁺] and [OH^-]. We can also define pOHThe negative logarithm of the hydroxide ion concentration. similar to pH:

pOH = -log[OH^-]

(In fact, p"anything" is defined as the negative logarithm of that anything.) This also implies that

[OH^-] = 10^-pOH

A simple and useful relationship is that for any aqueous solution,

pH + pOH = 14

This relationship makes it simple to determine pH from pOH or pOH from pH and then calculate the resulting ion concentration.

Example 14.3-3

The pH of a solution is 8.22. What are pOH, [H⁺], and [OH^-]?

Solution

Because the sum of pH and pOH equals 14, we have

8.22 + pOH = 14

Subtracting 8.22 from 14, we get

pOH = 5.78

Now we evaluate the following two expressions:

[H⁺] = 10^-8.22 [OH^-] = 10^-5.78

[H⁺] = 6.0 × 10^-9 M [OH^-] = 1.7 × 10^-6 M

Test Yourself

The pOH of a solution is 12.04. What are pH, [H⁺], and [OH^-]?

Answer

pH = 1.96; [H⁺] = 1.1 × 10^-2 M; [OH^-] = 9.1 × 10^-13 M

Key Equations

definition of pH

Equation 14.3(eq10): pH = −log[H⁺]

Equation 14.3(eq11): [H⁺] = 10^−pH

Acid–Base Properties of Solutions of Salts

We can also use the relative strengths of conjugate acid–base pairs to understand the acid–base properties of solutions of salts. A neutralization reaction can be defined as the reaction of an acid and a base to produce a salt and water. That is, another cation, such as Na⁺, replaces the proton on the acid. An example is the reaction of CH₃CO₂H, a weak acid, with NaOH, a strong base:

Equation 14.3(eq15)

\underset{acid}{{CH}_{3} {CO}_{2} H(l)} + \underset{base}{NaOH(s)} \overset{H_{2} O}{\to} \underset{salt}{{CH}_{3} {CO}_{2} Na(aq)} + \underset{water}{H_{2} O(l)}

Depending on the acid–base properties of its component ions, however, a salt can dissolve in water to produce a neutral solution, a basic solution, or an acidic solution.

When a salt such as NaCl dissolves in water, it produces Na⁺(aq) and Cl⁻(aq) ions. As the conjugate acid of a strong base(NaOH), the Na⁺ ion can be viewed as a very weak acid. The Cl⁻ ion is the conjugate base of the strong acid HCl, so it has essentially no basic character. Consequently, dissolving NaCl in water has no effect on the pH of a solution, and the solution remains neutral.

Now let's compare this behavior to the behavior of aqueous solutions of potassium cyanide and sodium acetate. Again, the cations (K⁺ and Na⁺) have essentially no acidic character, but the anions (CN⁻ and CH₃CO₂⁻) are weak bases that can react with water because they are the conjugate bases of the weak acids HCN and acetic acid, respectively.

Equation 14.3(eq16)

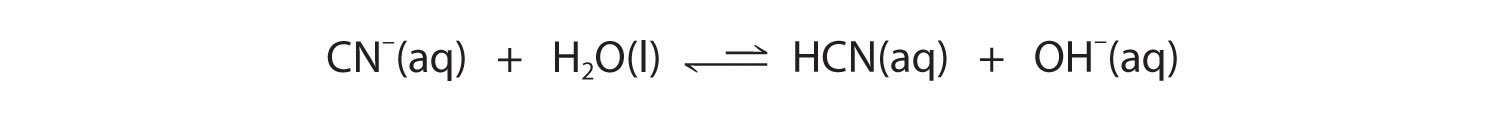
Equation 14.3(eq17)

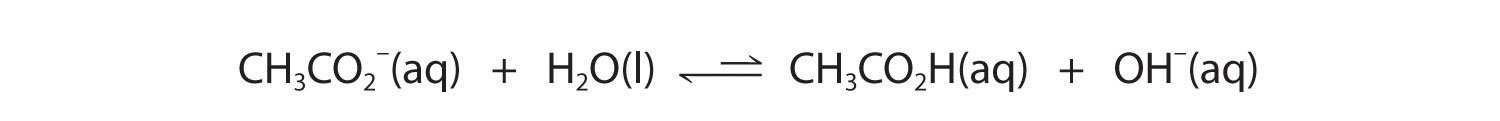
Neither reaction proceeds very far to the right as written because the formation of the weaker acid–base pair is favored. Both HCN and acetic acid are stronger acids than water, and hydroxide is a stronger base than either acetate or cyanide, so in both cases, the equilibrium lies to the left. Nonetheless, each of these reactions generates enough hydroxide ions to produce a basic solution. For example, the pH of a 0.1 M solution of sodium acetate or potassium cyanide at 25°C is 8.8 or 11.1, respectively. From Table 14.3(1) and Figure 14.3(a), we can see that CN⁻ is a stronger base (pK_b = 4.79) than acetate (pK_b = 9.24), which is consistent with KCN producing a more basic solution than sodium acetate at the same concentration.

In contrast, the conjugate acid of a weak base should be a weak acid (Figure 14.3(a)). For example, ammonium chloride and pyridinium chloride are salts produced by reacting ammonia and pyridine, respectively, with HCl. As you already know, the chloride ion is such a weak base that it does not react with water. In contrast, the cations of the two salts are weak acids that react with water as follows:

Equation 14.3(eq18)

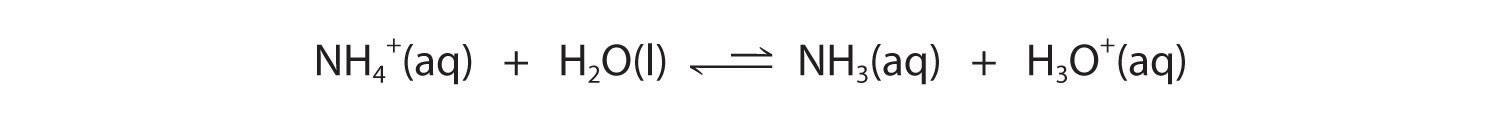
Equation 14.3(eq19)

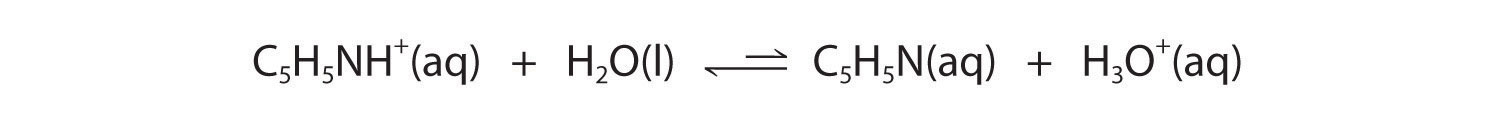
Figure 14.3(a) shows that H₃O⁺ is a stronger acid than either NH₄⁺ or C₅H₅NH⁺, and conversely, ammonia and pyridine are both stronger bases than water. The equilibrium will therefore lie far to the left in both cases, favoring the weaker acid–base pair. The H₃O⁺ concentration produced by the reactions is great enough, however, to decrease the pH of the solution significantly: the pH of a 0.10 M solution of ammonium chloride or pyridinium chloride at 25°C is 5.13 or 3.12, respectively. This is consistent with the information shown in Figure 14.3(a), indicating that the pyridinium ion is more acidic than the ammonium ion.

What happens with aqueous solutions of a salt such as ammonium acetate, where both the cation and the anion can react separately with water to produce an acid and a base, respectively? According to Equation 14.3(18), the ammonium ion will lower the pH, while according to Equation 14.3(17), the acetate ion will raise the pH. This particular case is unusual, in that the cation is as strong an acid as the anion is a base (pK_a ≈ pK_b). Consequently, the two effects cancel, and the solution remains neutral. With salts in which the cation is a stronger acid than the anion is a base, the final solution has a pH < 7.00. Conversely, if the cation is a weaker acid than the anion is a base, the final solution has a pH > 7.00.

Reactions such as those discussed in this section, in which a salt reacts with water to give an acidic or basic solution, are often called hydrolysis reactionsA chemical reaction in which a salt reacts with water to yield an acidic or a basic solution.. Using a separate name for this type of reaction is unfortunate because it suggests that they are somehow different. In fact, hydrolysis reactions are just acid–base reactions in which the acid is a cation or the base is an anion; they obey the same principles and rules as all other acid–base reactions.

Note the Pattern

A hydrolysis reaction is an acid–base reaction.

Example 14.3-4

Predict whether aqueous solutions of these compounds are acidic, basic, or neutral.

KNO₃
NH₄Br
Na₂SO₄

Given: compound

Asked for: acidity or basicity of aqueous solution

Strategy:

A Assess the acid–base properties of the cation and the anion. If the cation is the conjugate base of a strong acid, it will not affect the pH of the solution. If the cation is the conjugate acid of a weak base, however, it will react with water to produce an acidic solution.

B If the anion is the conjugate base of a strong acid, it will not affect the pH of the solution. If, however, the anion is the conjugate base of a weak acid, the solution will be basic.

Solution:

A The K⁺ cation is the conjugate acid of a strong base (KOH) and is therefore not going to effect pH.

B The NO₃⁻ anion is the conjugate base of a strong acid, so it has essentially no basic character. Hence neither the cation nor the anion will react with water to produce H⁺ or OH⁻, and the solution will be neutral.
A The NH₄⁺ ion is the conjugate acid of a weak base (NH₃), which will behave as a weak acid:

B The Br⁻ anion is a very weak base (it is the conjugate base of the strong acid HBr), so it does not affect the pH of the solution. Hence the solution will be acidic.
A The Na⁺ ion, like the K⁺, is a very weak acid, so it should not affect the acidity of the solution.

B In contrast, SO₄²⁻ is the conjugate base of HSO₄⁻, which is a weak acid. Hence the SO₄²⁻ ion will react with water as shown in Figure 16.6 to give a slightly basic solution.

Exercise

Predict whether aqueous solutions of the following are acidic, basic, or neutral.

KI
Ba(ClO₄)₂
NaHS

Answer:

neutral
neutral
basic (due to the reaction of HS⁻ with water to form H₂S and OH⁻)

Buffers

Weak acids are relatively common, even in the foods we eat. But we occasionally encounter a strong acid or base, such as stomach acid, which has a strongly acidic pH of 1.7. By definition, strong acids and bases can produce a relatively large amount of H⁺ or OH^- ions and consequently have marked chemical activities. In addition, very small amounts of strong acids and bases can change the pH of a solution very quickly. If 1 mL of stomach acid [approximated as 0.1 M HCl(aq)] were added to the bloodstream and no correcting mechanism were present, the pH of the blood would decrease from about 7.4 to about 4.7-a pH that is not conducive to continued living. Fortunately, the body has a mechanism for minimizing such dramatic pH changes.

The mechanism involves a bufferA solution that resists dramatic changes in pH., a solution that resists dramatic changes in pH. Buffers do so by being composed of certain pairs of solutes: either a weak acid plus a salt derived from that weak acid or a weak base plus a salt of that weak base. For example, a buffer can be composed of dissolved HC₂H₃O₂ (a weak acid) and NaC₂H₃O₂ (the salt derived from that weak acid). Another example of a buffer is a solution containing NH₃ (a weak base) and NH₄Cl (a salt derived from that weak base).

Let us use an HC₂H₃O₂/NaC₂H₃O₂ buffer to demonstrate how buffers work. If a strong base-a source of OH^-(aq) ions-is added to the buffer solution, those OH^- ions will react with the HC₂H₃O₂ in an acid-base reaction:

HC₂H₃O₂(aq) + OH^-(aq) → H₂O(l) + C₂H₃O₂^-(aq)

Rather than changing the pH dramatically by making the solution basic, the added OH^- ions react to make H₂O, so the pH does not change much.

If a strong acid-a source of H⁺ ions-is added to the buffer solution, the H⁺ ions will react with the anion from the salt. Because HC₂H₃O₂ is a weak acid, it is not ionized much. This means that if lots of H⁺ ions and C₂H₃O₂^- ions are present in the same solution, they will come together to make HC₂H₃O₂:

H⁺(aq) + C₂H₃O₂^-(aq) → HC₂H₃O₂(aq)

Rather than changing the pH dramatically and making the solution acidic, the added H⁺ ions react to make molecules of a weak acid. Figure 14.3(d) illustrates both actions of a buffer.

Figure 14.3(d) The Actions of Buffers

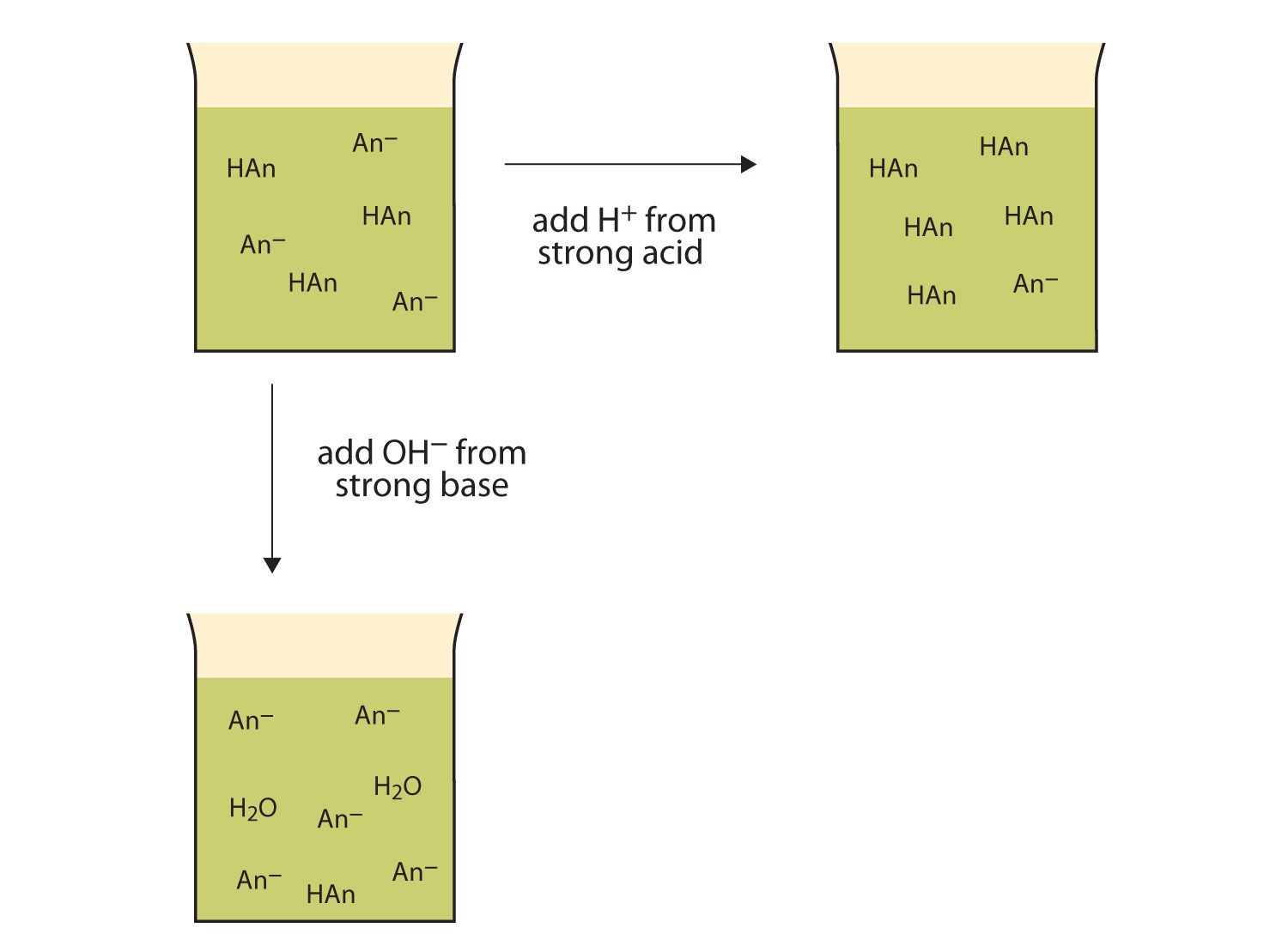
Buffers can react with both strong acids (top) and strong bases (side) to minimize large changes in pH.

Buffers made from weak bases and salts of weak bases act similarly. For example, in a buffer containing NH₃ and NH₄Cl, NH₃ molecules can react with any excess H⁺ ions introduced by strong acids:

NH₃(aq) + H⁺(aq) → NH₄⁺(aq)

while the NH₄⁺(aq) ion can react with any OH^- ions introduced by strong bases:

NH₄⁺(aq) + OH^-(aq) → NH₃(aq) + H₂O(l)

Example 14.3-6

Which combinations of compounds can make a buffer solution?

HCHO₂ and NaCHO₂
HCl and NaCl
CH₃NH₂ and CH₃NH₃Cl
NH₃ and NaOH

Solution

HCHO₂ is formic acid, a weak acid, while NaCHO₂ is the salt made from the anion of the weak acid (the formate ion [CHO₂^-]). The combination of these two solutes would make a buffer solution.
HCl is a strong acid, not a weak acid, so the combination of these two solutes would not make a buffer solution.
CH₃NH₂ is methylamine, which is like NH₃ with one of its H atoms substituted with a CH₃ group. Because it is not listed in Table 8.1(1), we can assume that it is a weak base. The compound CH₃NH₃Cl is a salt made from that weak base, so the combination of these two solutes would make a buffer solution.
NH₃ is a weak base, but NaOH is a strong base. The combination of these two solutes would not make a buffer solution.

Test Yourself

Which combinations of compounds can make a buffer solution?

NaHCO₃ and NaCl
H₃PO₄ and NaH₂PO₄
NH₃ and (NH₄)₃PO₄
NaOH and NaCl

Answers

Buffers work well only for limited amounts of added strong acid or base. Once either solute is completely reacted, the solution is no longer a buffer, and rapid changes in pH may occur. We say that a buffer has a certain capacityThe amount of strong acid or base a buffer can counteract.. Buffers that have more solute dissolved in them to start with have larger capacities, as might be expected.

Human blood has a buffering system to minimize extreme changes in pH. One buffer in blood is based on the presence of HCO₃^- and H₂CO₃ [the second compound is another way to write CO₂(aq)]. With this buffer present, even if some stomach acid were to find its way directly into the bloodstream, the change in the pH of blood would be minimal. Inside many of the body's cells, there is a buffering system based on phosphate ions.

Key Takeaway

A buffer is a solution that resists sudden changes in pH.

Summary

Two species that differ by only a proton constitute a conjugate acid–base pair. The magnitude of the equilibrium constant for an ionization reaction can be used to determine the relative strengths of acids and bases. For an aqueous solution of a weak acid, the dissociation constant is called the acid ionization constant (K_a). Smaller values of pK_a correspond to larger acid ionization constants and hence stronger acids. No acid stronger than H₃O⁺ and no base stronger than OH⁻ can exist in aqueous solution, leading to the phenomenon known as the leveling effect. The acidity or basicity of an aqueous solution is described quantitatively using the pH scale. The pH of a solution is the negative logarithm of the H⁺ ion concentration and typically ranges from 0 for strongly acidic solutions to 14 for strongly basic ones. Because of the autoionization reaction of water, which produces small amounts of hydronium ions and hydroxide ions, a neutral solution of water contains 1 × 10⁻⁷ M H⁺ ions and has a pH of 7.0. An indicator is an intensely colored organic substance whose color is pH dependent; it is used to determine the pH of a solution. A salt can dissolve in water to produce a neutral, a basic, or an acidic solution, depending on whether it contains the conjugate base of a weak acid as the anion (A⁻), the conjugate acid of a weak base as the cation (BH⁺), or both. The reaction of a salt with water to produce an acidic or a basic solution is called a hydrolysis reaction. Buffer solutions resist a change in pH despite the addition of acid or base. Buffered solutions are composed of either a weak acid and its salt or a weak base and its salt.

Conceptual Problems

Identify the conjugate acid–base pairs in each equilibrium.
1. ${HSO}_{4}^{-} (aq) + H_{2} O(l) ⇌ {SO}_{4}^{2 -} (aq) + H_{3} O^{+} (aq)$
2. $C_{3} H_{7} {NO}_{2} (aq) + H_{3} O^{+} (aq) ⇌ C_{3} H_{8} {NO}_{2}^{+} (aq) + H_{2} O(l)$
3. ${CH}_{3} {CO}_{2} H(aq) + {NH}_{3} (aq) ⇌ {CH}_{3} {CO}_{2}^{-} (aq) + {NH}_{4}^{+} (aq)$
4. ${SbF}_{5} (aq) + 2 HF(aq) ⇌ H_{2} F^{+} (aq) + {SbF}_{6}^{-} (aq)$
Identify the conjugate acid–base pairs in each equilibrium.
1. $HF(aq) + H_{2} O(l) ⇌ H_{3} O^{+} (aq) + F^{-} (aq)$
2. ${CH}_{3} {CH}_{2} {NH}_{2} (aq) + H_{2} O(l) ⇌ {CH}_{3} {CH}_{2} {NH}_{3}^{+} (aq) + {OH}^{-} (aq)$
3. $C_{3} H_{7} {NO}_{2} (aq) + {OH}^{-} (aq) ⇌ C_{3} H_{6} {NO}_{2}^{-} (aq) + H_{2} O(l)$
4. ${CH}_{3} {CO}_{2} H(aq) + 2 HF(aq) ⇌ {CH}_{3} {C(OH)}_{2}^{+} (aq) + {HF}_{2}^{-} (aq)$
Salts such as NaH contain the hydride ion (H⁻). When sodium hydride is added to water, it produces hydrogen gas in a highly vigorous reaction. Write a balanced chemical equation for this reaction and identify the conjugate acid–base pairs.
Write the expression for K_a for each reaction.
1. ${HCO}_{3}^{-} (aq) + H_{2} O(l) ⇌ {CO}_{3}^{2 -} (aq) + H_{3} O^{+} (aq)$
2. $formic acid(aq) + H_{2} O(l) ⇌ formate(aq) + H_{3} O^{+} (aq)$
3. $H_{3} {PO}_{4} (aq) + H_{2} O(l) ⇌ H_{2} {PO}_{4}^{-} (aq) + H_{3} O^{+} (aq)$
Is it accurate to say that a 2.0 M solution of H₂SO₄, which contains two acidic protons per molecule, is 4.0 M in H⁺? Explain your answer.
Why are aqueous solutions of salts such as CaCl₂ neutral? Why is an aqueous solution of NaNH₂ basic?
Predict whether aqueous solutions of the following are acidic, basic, or neutral.
1. Li₃N
2. NaH
3. KBr
4. C₂H₅NH₃⁺Cl⁻
When each compound is added to water, would you expect the pH of the solution to increase, decrease, or remain the same?
1. LiCH₃
2. MgCl₂
3. K₂O
4. (CH₃)₂NH₂⁺Br⁻
Define buffer. What two related chemical components are required to make a buffer?
Can a buffer be made by combining a strong acid with a strong base? Why or why not?
Which combinations of compounds can make a buffer? Assume aqueous solutions.
1. HCl and NaCl
2. HNO₂ and NaNO₂
3. NH₄NO₃ and HNO₃
4. NH₄NO₃ and NH₃
Which combinations of compounds can make a buffer? Assume aqueous solutions.
1. H₃PO₄ and Na₃PO₄
2. NaHCO₃ and Na₂CO₃
3. NaNO₃ and Ca(NO₃)₂
4. HN₃ and NH₃
For each combination in Conceptual Problem 11 that is a buffer, write the chemical equations for the reactions of the buffer components when a strong acid and a strong base is added.
For each combination in Conceptual Problem 12 that is a buffer, write the chemical equations for the reactions of the buffer components when a strong acid and a strong base is added.
The complete phosphate buffer system is based on four substances: H₃PO₄, H₂PO₄^-, HPO₄^2-, and PO₄^3-. What different buffer solutions can be made from these substances?
Explain why NaBr cannot be a component in either an acidic or a basic buffer.
Two solutions are made containing the same concentrations of solutes. One solution is composed of H₃PO₄ and Na₃PO₄, while the other is composed of HCN and NaCN. Which solution should have the larger capacity as a buffer?
Two solutions are made containing the same concentrations of solutes. One solution is composed of NH₃ and NH₄NO₃, while the other is composed of H₂SO₄ and Na₂SO₄. Which solution should have the larger capacity as a buffer?

Answers

1. $\overset{acid 1}{{HSO}_{4}^{-} (aq)} + \underset{base 2}{H_{2} O(l)} ⇌ \overset{base 1}{{SO}_{4}^{2 -} (aq)} + \underset{acid 2}{H_{3} O^{+} (aq)}$
2. $\underset{base 2}{C_{3} H_{7} {NO}_{2} (aq)} + \overset{acid 1}{H_{3} O^{+} (aq)} ⇌ \underset{acid 2}{C_{3} H_{8} {NO}_{2}^{+} (aq)} + \overset{base 1}{H_{2} O(l)}$
3. $\overset{acid 1}{HOAc(aq)} + \underset{base 2}{{NH}_{3} (aq)} ⇌ \overset{base 1}{{CH}_{3} {CO}_{2}^{-} (aq)} + \underset{acid 2}{{NH}_{4}^{+} (aq)}$
4. $\overset{acid 1}{{SbF}_{5} (aq)} + \underset{base 2}{2 HF(aq)} ⇌ \underset{acid 2}{H_{2} F^{+} (aq)} + \overset{base 1}{{SbF}_{6}^{-} (aq)}$
H₂O + NaH→ H₂ + NaOH; HOH/OH^- and H₂/H^-
It would not be accurate to say 2M H₂SO₄ is 4M in H⁺. HSO₄^- is a weak acid. In water, only a fraction of the HSO₄^- will dissociate.
1. basic
2. basic
3. neutral
4. acidic
A buffer is the combination of a weak acid or base and a salt of that weak acid or base.
1. no
2. yes
3. no
4. yes
3b: strong acid: NO₂^- + H⁺ → HNO₂; strong base: HNO₂ + OH^- → NO₂^- + H₂O; 3d: strong base: NH₄⁺ + OH^- → NH₃ + H₂O; strong acid: NH₃ + H⁺ → NH₄⁺
Buffers can be made from three combinations: (1) H₃PO₄ and H₂PO₄^-, (2) H₂PO₄^- and HPO₄^2-, and (3) HPO₄^2- and PO₄^3-. (Technically, a buffer can be made from any two components.)
The phosphate buffer should have the larger capacity.

Numerical Problems

Arrange these acids in order of increasing strength.
- acid A: pK_a = 1.52
- acid B: pK_a = 6.93
- acid C: pK_a = 3.86
Given solutions with the same initial concentration of each acid, which would have the highest percent ionization?
At 298K, pK_a + pK_b = 14. Arrange these bases in order of increasing strength:
- base A: pK_b = 13.10
- base B: pK_b = 8.74
- base C: pK_b = 11.87
Given solutions with the same initial concentration of each base, which would have the highest percent ionization?
Calculate the K_a and the pK_a of the conjugate acid of a base with each pK_b value.
1. 3.80
2. 7.90
3. 13.70
4. 1.40
5. −2.50
Benzoic acid is a food preservative with a pK_a of 4.20. Determine the K_b and the pK_b for the benzoate ion.
Determine K_a and pK_a of boric acid [B(OH)₃], solutions of which are occasionally used as an eyewash; the pK_b of its conjugate base is 4.80.
Define pH. How is it related to pOH?
Define pOH. How is it related to pH?
What is the pH range for an acidic solution?
What is the pH range for a basic solution?
What is [H⁺] for a neutral solution?
What is [OH^-] for a neutral solution? Compare your answer to Numerical Problem 10. Does this make sense?
Which substances in Figure 14.3(b) are acidic?
Which substances in Figure 14.3(b) are basic?
What is the pH of a solution when [H⁺] is 3.44 × 10^-4 M?
What is the pH of a solution when [H⁺] is 9.04 × 10^-13 M?
What is the pH of a solution when [OH^-] is 6.22 × 10^-7 M?
What is the pH of a solution when [OH^-] is 0.0222 M?
What is the pOH of a solution when [H⁺] is 3.44 × 10^-4 M?
What is the pOH of a solution when [H⁺] is 9.04 × 10^-13 M?
What is the pOH of a solution when [OH^-] is 6.22 × 10^-7 M?
What is the pOH of a solution when [OH^-] is 0.0222 M?
If a solution has a pH of 0.77, what is its pOH, [H⁺], and [OH^-]?
If a solution has a pOH of 13.09, what is its pH, [H⁺], and [OH^-]?

Answers

acid B < acid C < acid A (strongest)
1. K_a = 6.3 × 10⁻¹¹; pK_a = 10.20
2. K_a = 7.9 × 10⁻⁷; pK_a = 6.10
3. K_a = 0.50; pK_a = 0.30
4. K_a = 2.5 × 10⁻¹³; pK_a = 12.60
5. K_a = 3.2 × 10⁻¹⁷; pK_a = 16.50
K_a = 6.3 × 10⁻¹⁰ pK_a = 9.20
pH is the negative logarithm of [H⁺] and is equal to 14 - pOH.
pH < 7
1.0 × 10^-7 M
Every entry above pure water is acidic.
3.46
7.79
10.54
6.21
pOH = 13.23; [H⁺] = 1.70 × 10^-1 M; [OH^-] = 5.89 × 10^-14 M

14.3 Acid-Base Properties of Solutions

Learning Objectives

Conjugate Acid–Base Pairs

Note the Pattern

Acid–Base Equilibrium Constants: Ka and pKa

Note the Pattern

Solutions of Strong Acids and Bases: The Leveling Effect

Note the Pattern

The pH Scale

Note the Pattern

Example 14.3-1

Example 14.3-2

Example 14.3-3

Key Equations

Acid–Base Properties of Solutions of Salts

Note the Pattern

Example 14.3-4

Buffers

Example 14.3-6

Key Takeaway

Summary

Conceptual Problems

Answers

Numerical Problems

Answers

Acid–Base Equilibrium Constants: K_a and pK_a