This is "Unit 10", section 10.1 from the book General Chemistry (v. 1.0).
10.1 Stoichiometry
Learning Objective
- To calculate the quantities of compounds produced or consumed in a chemical reaction.
Consider a classic recipe for pound cake: 1 pound of eggs, 1 pound of butter, 1 pound of flour, and 1 pound of sugar. (That's why it's called pound cake.) If you have 4 pounds of butter, how many pounds of sugar, flour, and eggs do you need? You would need 4 pounds each of sugar, flour, and eggs.
Now suppose you have 1.00 g H2. If the chemical reaction follows the balanced chemical equation
2H2(g) + O2(g) → 2H2O(l)then what mass of oxygen do you need to make water?
Curiously, this chemical reaction question is very similar to the pound cake question. Both of them involve relating a quantity of one substance to a quantity of another substance or substances. The relating of one chemical substance to another using a balanced chemical reaction is called stoichiometryThe relating of one chemical substance to another using a balanced chemical equation.. Using stoichiometry is a fundamental skill in chemistry; it greatly broadens your ability to predict what will occur and, more importantly, how much is produced.
Let us consider a more complicated example. A recipe for pancakes calls for 2 cups (c) of pancake mix, 1 egg, and 1/2 c of milk. We can write this in the form of a chemical equation:
2 c mix + 1 egg + 1/2 c milk → 1 batch of pancakesIf you have 9 c of pancake mix, how many eggs and how much milk do you need? It might take a little bit of work, but eventually you will find you need 4½ eggs and 2¼ c milk.
How can we formalize this? We can make a conversion factor using our original recipe and use that conversion factor to convert from a quantity of one substance to a quantity of another substance, similar to the way we constructed a conversion factor between grams and milligrams in Chapter 2 "Dimensional Analysis". Because one recipe's worth of pancakes requires 2 c of pancake mix, 1 egg, and 1/2 c of milk, we actually have the following mathematical relationships that relate these quantities:
2 c pancake mix = 1 egg =1/2 c milkThese are the equivalent quantities needed for a single recipe of pancakes. So, any possible quantities of two or more ingredients must have the same numerical ratio as the ratios in the equivalence.
We can deal with these equivalences in the same way we deal with equalities in unit conversions: we can make conversion factors that essentially equal 1. For example, to determine how many eggs we need for 9 c of pancake mix, we construct the conversion factor
This conversion factor is, in a strange way, equivalent to 1 because the recipe relates the two quantities. Starting with our initial quantity and multiplying by our conversion factor,
Note how the units cups pancake mix canceled, leaving us with units of eggs. This is the formal, mathematical way of getting our amounts to mix with 9 c of pancake mix. We can use a similar conversion factor for the amount of milk:
Again, units cancel, and new units are introduced.
A balanced chemical equation is nothing more than a recipe for a chemical reaction. The difference is that a balanced chemical equation is written in terms of atoms and molecules, not cups, pounds, and eggs.
For example, consider the following chemical equation:
2H2(g) + O2(g) → 2H2O(l)We can interpret this as, literally, "two hydrogen molecules react with one oxygen molecule to make two water molecules." That interpretation leads us directly to some equivalences, just as our pancake recipe did:
2H2 molecules = 1O2 molecule = 2H2O moleculesThese equivalences allow us to construct conversion factors:
and so forth. These conversions can be used to relate quantities of one substance to quantities of another. For example, suppose we need to know how many molecules of oxygen are needed to react with 16 molecules of H2. As we did with converting units, we start with our given quantity and use the appropriate conversion factor:
Note how the unit molecules H2 cancels algebraically, just as any unit does in a conversion like this. The conversion factor came directly from the coefficients in the balanced chemical equation. This is another reason why a properly balanced chemical equation is important.
Example 10.1-1
How many molecules of SO3 are needed to react with 144 molecules of Fe2O3 given this balanced chemical equation?
Fe2O3(s) + 3SO3(g) → Fe2(SO4)3Solution
We use the balanced chemical equation to construct a conversion factor between Fe2O3 and SO3. The number of molecules of Fe2O3 goes on the bottom of our conversion factor so it cancels with our given amount, and the molecules of SO3 go on the top. Thus, the appropriate conversion factor is
Starting with our given amount and applying the conversion factor, the result is
We need 432 molecules of SO3 to react with 144 molecules of Fe2O3.
Test Yourself
How many molecules of H2 are needed to react with 29 molecules of N2 to make ammonia if the balanced chemical equation is N2 + 3H2 → 2NH3?
Answer
87 molecules
Recall Section 7.1, where you learned how to write the balanced equation for the reaction of the ammonium dichromate volcano in terms of the atoms, ions, or molecules involved. That was stoichiometry. But working with small numbers of atoms and molecules is not terribly practical. Instead, chemists work with amounts of substances in grams or moles. Now it's time to see how to use the stoichiometry of a reaction to answer questions like the following: How many pounds of oxygen is needed to ensure complete combustion of a pound of isooctane? (This information is crucial to the design of nonpolluting and efficient automobile engines.) How many grams of pure gold can be obtained from a ton of low-grade gold ore? (The answer determines whether the ore deposit is worth mining.) If an industrial plant must produce a certain number of tons of sulfuric acid per week, how much elemental sulfur must arrive by rail each week?
All these questions can be answered using the concepts of the mole and molar and formula masses, along with the coefficients in the appropriate balanced chemical equation.
Stoichiometry Problems
When we carry out a reaction in either an industrial setting or a laboratory, it is easier to work with masses of substances than with the numbers of molecules or moles. The general method for converting from the mass of any reactant or product to the mass of any other reactant or product using a balanced chemical equation is outlined in and described in the following text.
Steps in Converting between Masses of Reactant and Product
- Convert the mass of one substance (substance A) to the corresponding number of moles using its molar mass.
- From the balanced chemical equation, obtain the number of moles of another substance (B) from the number of moles of substance A using the appropriate mole ratio (the ratio of their coefficients).
- Convert the number of moles of substance B to mass using its molar mass. It is important to remember that some species are in excess by virtue of the reaction conditions. For example, if a substance reacts with the oxygen in air, then oxygen is in obvious (but unstated) excess.
Converting amounts of substances to moles—and vice versa—is the key to all stoichiometry problems, whether the amounts are given in units of mass (grams or kilograms), weight (pounds or tons), or volume (liters or gallons).
Figure 10.1(a) A Flowchart for Stoichiometric Calculations Involving Pure Substances
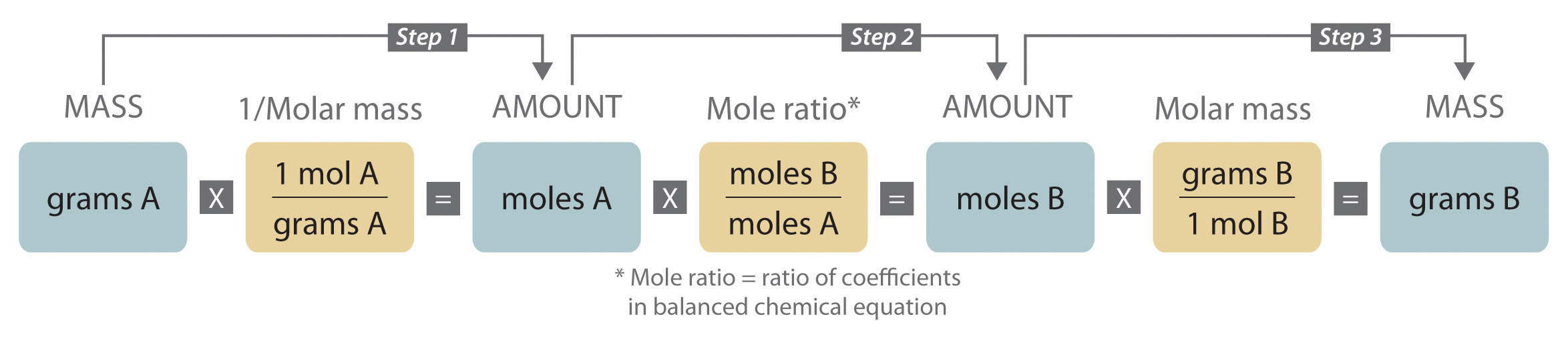
The molar masses of the reactants and the products are used as conversion factors so that you can calculate the mass of product from the mass of reactant and vice versa.
To illustrate this procedure, let’s return to the combustion of glucose. We saw earlier that glucose reacts with oxygen to produce carbon dioxide and water:
Equation 10.1(eq1)
C6H12O6(s) + 6O2(g) → 6CO2(g) + 6H2O(l)Just before a chemistry exam, suppose a friend reminds you that glucose is the major fuel used by the human brain. You therefore decide to eat a candy bar to make sure that your brain doesn’t run out of energy during the exam (even though there is no direct evidence that consumption of candy bars improves performance on chemistry exams). If a typical 2 oz candy bar contains the equivalent of 45.3 g of glucose and the glucose is completely converted to carbon dioxide during the exam, how many grams of carbon dioxide will you produce and exhale into the exam room?
The initial step in solving a problem of this type must be to write the balanced chemical equation for the reaction. Inspection of Equation 10.1(eq1) shows that it is balanced as written, so we can proceed to the strategy outlined in Figure 10.1(a) , adapting it as follows:
Use the molar mass of glucose (to one decimal place, 180.2 g/mol) to determine the number of moles of glucose in the candy bar:
According to the balanced chemical equation, 6 mol of CO2 is produced per mole of glucose; the mole ratio of CO2 to glucose is therefore 6:1. The number of moles of CO2 produced is thus
Use the molar mass of CO2 (44.010 g/mol) to calculate the mass of CO2 corresponding to 1.51 mol of CO2:
We can summarize these operations as follows:
Discrepancies between the two values are attributed to rounding errors resulting from using stepwise calculations in steps 1–3. In Chapter 12, you will discover that this amount of gaseous carbon dioxide occupies an enormous volume—more than 33 L. We could use similar methods to calculate the amount of oxygen consumed or the amount of water produced.
We just used the balanced chemical equation to calculate the mass of product that is formed from a certain amount of reactant. We can also use the balanced chemical equation to determine the masses of reactants that are necessary to form a certain amount of product or, as shown in Example 10.1-2, the mass of one reactant that is required to consume a given mass of another reactant.
Example 10.1-2
The combustion of hydrogen with oxygen to produce gaseous water is extremely vigorous, producing one of the hottest flames known. Because so much energy is released for a given mass of hydrogen or oxygen, this reaction was used to fuel the NASA (National Aeronautics and Space Administration) space shuttles, which have recently been retired from service. NASA engineers calculated the exact amount of each reactant needed for the flight to make sure that the shuttles did not carry excess fuel into orbit. Calculate how many tons of hydrogen a space shuttle needed to carry for each 1.00 tn of oxygen (1 tn = 2000 lb).

The US space shuttle Discovery during liftoff. The large cylinder in the middle contains the oxygen and hydrogen that fueled the shuttle’s main engine. STS-39 Discovery, Orbiter Vehicle (OV) 103, lifts off from a Kennedy Space Center (KSC) Launch Complex (LC) Pad 39A at 7:33:14 am (Eastern Daylight Time (EDT) May 7, 1991). OV-103 atop the external tank (ET) and flanked by its two solid rocket boosters (SRBs) is partially obscured by the retracted rotating service structure (RSS) in the foreground as it leaves the mobile launcher platform and before it clears the launch tower fixed service structure (FSS). An exhaust cloud created by the SRB and space shuttle main engine (SSME) firings fills the launch pad area. This image file is in the public domain in the United States because it was solely created by NASA.
Given: reactants, products, and mass of one reactant
Asked for: mass of other reactant
Strategy:
A Write the balanced chemical equation for the reaction.
B Convert mass of oxygen to moles. From the mole ratio in the balanced chemical equation, determine the number of moles of hydrogen required. Then convert the moles of hydrogen to the equivalent mass in tons.
Solution:
We use the same general strategy for solving stoichiometric calculations as in the preceding example. Because the amount of oxygen is given in tons rather than grams, however, we also need to convert tons to units of mass in grams. Another conversion is needed at the end to report the final answer in tons.
A We first use the information given to write a balanced chemical equation. Because we know the identity of both the reactants and the product, we can write the reaction as follows:
H2(g) + O2(g) → H2O(g)This equation is not balanced because there are two oxygen atoms on the left side and only one on the right. Assigning a coefficient of 2 to both H2O and H2 gives the balanced chemical equation:
2H2(g) + O2(g) → 2H2O(g)Thus 2 mol of H2 react with 1 mol of O2 to produce 2 mol of H2O.
B To convert tons of oxygen to units of mass in grams, we multiply by the appropriate conversion factors:
Using the molar mass of O2 (32.00 g/mol, to four significant figures), we can calculate the number of moles of O2 contained in this mass of O2:
Now use the coefficients in the balanced chemical equation to obtain the number of moles of H2 needed to react with this number of moles of O2:
The molar mass of H2 (2.016 g/mol) allows us to calculate the corresponding mass of H2:
Finally, convert the mass of H2 to the desired units (tons) by using the appropriate conversion factors:
The space shuttle had to be designed to carry 0.126 tn of H2 for each 1.00 tn of O2. Even though 2 mol of H2 are needed to react with each mole of O2, the molar mass of H2 is so much smaller than that of O2 that only a relatively small mass of H2 is needed compared to the mass of O2.
Exercise
Alchemists produced elemental mercury by roasting the mercury-containing ore cinnabar (HgS) in air:
HgS(s) + O2(g) → Hg(l) + SO2(g)The volatility and toxicity of mercury make this a hazardous procedure, which likely shortened the life span of many alchemists. Given 100 g of cinnabar, how much elemental mercury can be produced from this reaction?
Answer: 86.2 g
Summary
The stoichiometry of a reaction describes the relative amounts of reactants and products in a balanced chemical equation. A stoichiometric quantity of a reactant is the amount necessary to react completely with the other reactant(s). /p>
Key Takeaway
- The stoichiometry of a balanced chemical equation identifies the maximum amount of product that can be obtained.
Numerical Problems
-
Think back to the pound cake recipe. What possible conversion factors can you construct relating the components of the recipe?
-
Think back to the pancake recipe. What possible conversion factors can you construct relating the components of the recipe?
-
What are all the conversion factors that can be constructed from the balanced chemical reaction 2H2(g) + O2(g) → 2H2O(l)?
-
What are all the conversion factors that can be constructed from the balanced chemical reaction N2(g) + 3H2(g) → 2NH3(g)?
-
Given the chemical equation
Na(s) + H2O(l) → NaOH(aq) + H2(g)- Balance the equation.
- How many molecules of H2 are produced when 332 atoms of Na react?
-
Given the chemical equation
S(s) + O2(g) → SO3(g)- Balance the equation.
- How many molecules of O2 are needed when 38 atoms of S react?
-
For the balanced chemical equation
6H+(aq) + 2MnO4-(aq) + 5H2O2(aq) → 2Mn2+(aq) + 5O2(g) + 8H2O(l)how many molecules of H2O are produced when 75 molecules of H2O2 react?
-
For the balanced chemical reaction
2C6H6(l) + 15O2(g) → 12CO2(g) + 6H2O(l)how many molecules of CO2 are produced when 56 molecules of C6H6 react?
-
Given the balanced chemical equation
Fe2O3(s) + 3SO3(g) → Fe2(SO4)3how many molecules of Fe2(SO4)3 are produced if 321 atoms of S are reacted?
-
For the balanced chemical equation
CuO(s) + H2S(g) → CuS + H2O(l)how many molecules of CuS are formed if 9,044 atoms of H react?
-
For the balanced chemical equation
Fe2O3(s) + 3SO3(g) → Fe2(SO4)3suppose we need to make 145,000 molecules of Fe2(SO4)3. How many molecules of SO3 do we need?
-
One way to make sulfur hexafluoride is to react thioformaldehyde, CH2S, with elemental fluorine:
CH2S + 6F2 → CF4 + 2HF + SF6If 45,750 molecules of SF6 are needed, how many molecules of F2 are required?
-
Construct the three independent conversion factors possible for these two reactions:
- 2H2 + O2 → 2H2O
- H2 + O2 → H2O2
Why are the ratios between H2 and O2 different?
The conversion factors are different because the stoichiometries of the balanced chemical reactions are different.
-
Construct the three independent conversion factors possible for these two reactions:
- 2Na + Cl2 → 2NaCl
- 4Na + 2Cl2 → 4NaCl
What similarities, if any, exist in the conversion factors from these two reactions?
-
Determine the mass of each reactant needed to give the indicated amount of product. Be sure that the chemical equations are balanced.
- AgNO3(aq) + CaCl2(s) → AgCl(s) + Ca(NO3)2(aq); 1.25 mol of AgCl
- Pb(s) + PbO2(s) + H2SO4(aq) → PbSO4(s) + H2O(l); 3.8 g of PbSO4
- H3PO4(aq) + MgCO3(s) → Mg3(PO4)2(s) + CO2(g) + H2O(l); 6.41 g of Mg3(PO4)2
-
Under certain conditions, the reaction of hydrogen with carbon monoxide can produce methanol.
- Write a balanced chemical equation for this reaction.
- Calculate the percent yield if exactly 200 g of methanol is produced from exactly 300 g of carbon monoxide.
-
Chlorine dioxide is a bleaching agent used in the paper industry. It can be prepared by the following reaction:
NaClO2(s) + Cl2(g) → ClO2(aq) + NaCl(aq)- What mass of chlorine is needed for the complete reaction of 30.5 g of NaClO2?
-
Calculate the number of grams of magnesium chloride that could be obtained from 7.50 g of hydrochloric acid when the latter is reacted with an excess of magnesium oxide.
-
Calculate the number of grams of oxygen that will react with 14.2 g of calcium to form CaO.
Answers
-
or are two conversion factors that can be constructed from the pound cake recipe. Other conversion factors are also possible.
-
-
, , , and their reciprocals are the conversion factors that can be constructed.
-
-
- 2Na(s) + 2H2O(l) → 2NaOH(aq) + H2(g)
- 166 molecules
-
-
120 molecules
-
-
107 molecules
-
-
435,000 molecules
-
-
- , , and
- , , and
-
-
- 212 g AgNO3, 69.4 g CaCl2
- 1.30 g Pb, 1.50 g PbO2, 1.23 g H2SO4
- 4.78 g H3PO4, 6.17 g MgCO3
-
-
12.0 g
-
-






