One assumption we have made about chemical reactions-in addition to the assumption that reactions proceed all the way to completion-is that all the reactants are present in the proper quantities to react to products. This is not always the case.

In all the examples discussed thus far, the reactants were assumed to be present in stoichiometric quantities. Consequently, none of the reactants was left over at the end of the reaction. This is often desirable, as in the case of a space shuttle, where excess oxygen or hydrogen was not only extra freight to be hauled into orbit but also an explosion hazard. More often, however, reactants are present in mole ratios that are not the same as the ratio of the coefficients in the balanced chemical equation. As a result, one or more of them will not be used up completely but will be left over when the reaction is completed. In this situation, the amount of product that can be obtained is limited by the amount of only one of the reactants. The reactant that restricts the amount of product obtained is called the limiting reactantThe reactant that restricts the amount of product obtained in a chemical reaction.. The reactant that remains after a reaction has gone to completion is in excess.

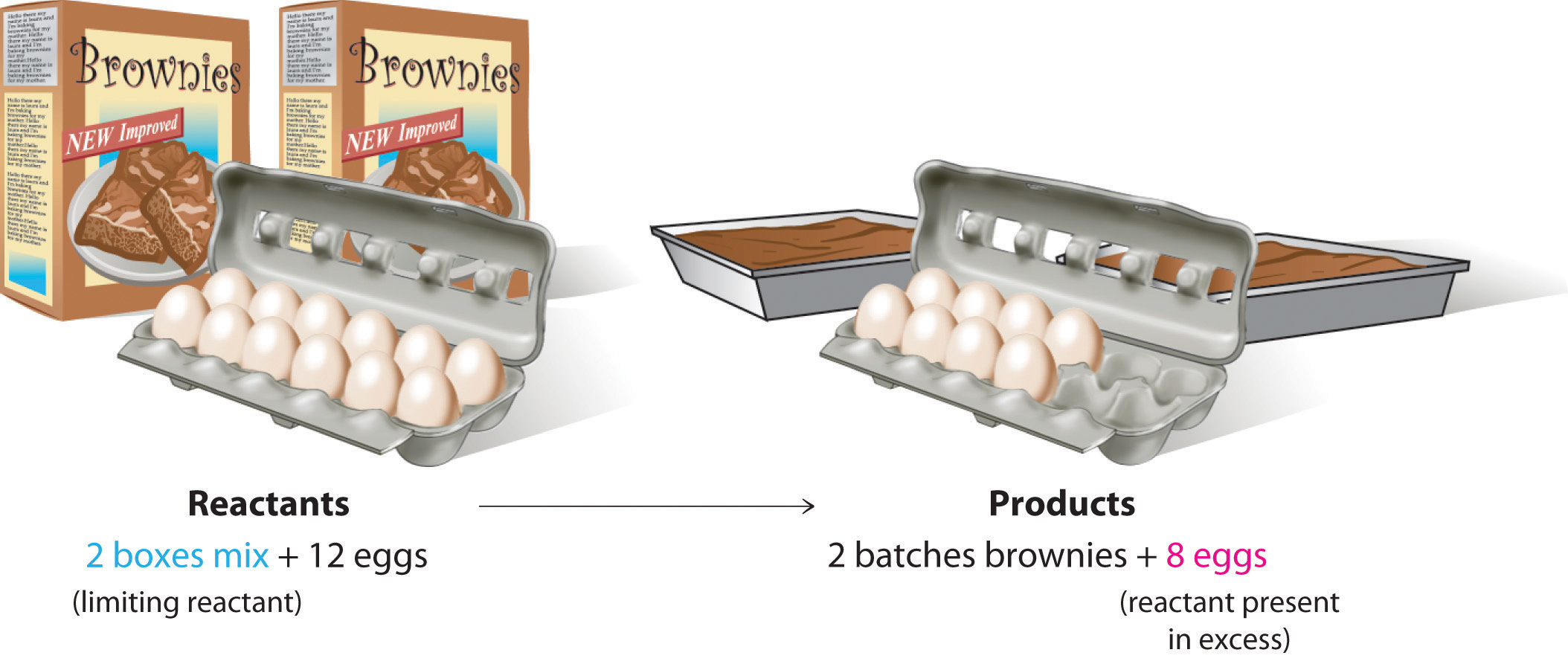
To be certain you understand these concepts, let’s first consider a nonchemical example. Assume you have invited some friends for dinner and want to bake brownies for dessert. You find two boxes of brownie mix in your pantry and see that each package requires two eggs. The balanced equation for brownie preparation is thus

If you have a dozen eggs, which ingredient will determine the number of batches of brownies that you can prepare? Because each box of brownie mix requires two eggs and you have two boxes, you need four eggs. Twelve eggs is eight more eggs than you need. Although the ratio of eggs to boxes in is 2:1, the ratio in your possession is 6:1. Hence the eggs are the ingredient (reactant) present in excess, and the brownie mix is the limiting reactant. Even if you had a refrigerator full of eggs, you could make only two batches of brownies.

Figure 10.2(a) The Concept of a Limiting Reactant in the Preparation of Brownies

Consider Figure 10.2(b) "Making Water". Here we are taking hydrogen atoms and oxygen atoms (left) to make water molecules (right). However, there are not enough oxygen atoms to use up all the hydrogen atoms. We run out of oxygen atoms and cannot make any more water molecules, so the process stops when we run out of oxygen atoms.

Figure 10.2(b) Making Water

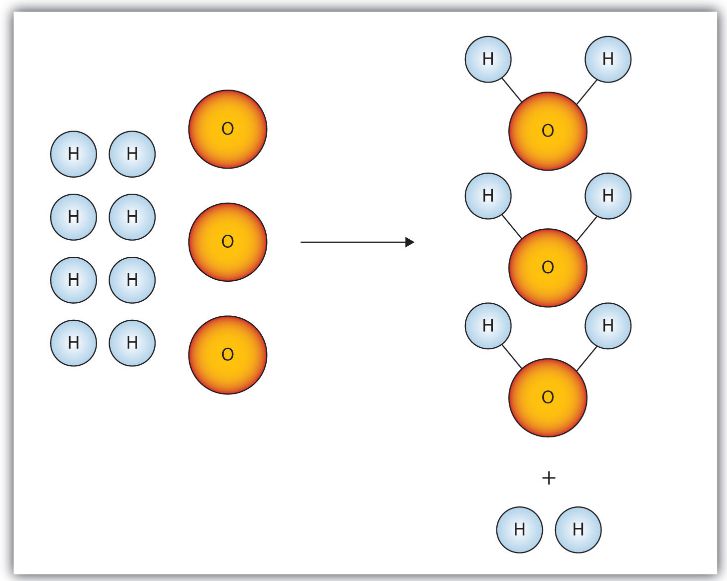
In this strictly illustrative scenario for making water molecules, we run out of O atoms before we use up all the H atoms. Similar situations exist for many chemical reactions when one reactant runs out before the other.

A similar situation exists for many chemical reactions: you usually run out of one reactant before all of the other reactant has reacted. The reactant you run out of is called the limiting reagentThe reactant that runs out first.; the other reactant or reactants are considered to be in excess. A crucial skill in evaluating the conditions of a chemical process is to determine which reactant is the limiting reagent and which is in excess.

The key to recognizing which reactant is the limiting reagent is based on a stoichiometric calculation using the mole ratio: whichever reactant gives the lesser amount of product is the limiting reagent. What we need to do is determine an amount of one product (either moles or mass) assuming all of each reactant reacts. Whichever reactant gives the least amount of that particular product is the limiting reagent. It does not matter which product we use, as long as we use the same one each time. It does not matter whether we determine the number of moles or grams of that product; however, we will see shortly that knowing the final mass of product can be useful.

For example, consider this reaction:

Suppose we start a reaction with 50.0 g of As and 50.0 g of O₂. Which one is the limiting reagent? We need to perform two mole-mass calculations, each assuming that each reactant reacts completely. Then we compare the amount of the product produced by each and determine which is less.

The calculations are as follows:

Comparing these two answers, it is clear that 0.334 mol of As₂O₃ is less than 1.04 mol of As₂O₃, so arsenic is the limiting reagent. If this reaction is performed under these initial conditions, the arsenic will run out before the oxygen runs out. We say that the oxygen is "in excess."

Identifying the limiting reagent, then, is straightforward. However, there are usually two associated questions: (1) what mass of product (or products) is then actually formed? and (2) what mass of what reactant is left over? The first question is straightforward to answer: simply perform a conversion from the number of moles of product formed to its mass, using its molar mass. For As₂O₃, the molar mass is 197.84 g/mol; knowing that we will form 0.334 mol of As₂O₃ under the given conditions, we will get

The second question is somewhat more convoluted to answer. First, we must do a mass-mass calculation relating the limiting reagent (here, As) to the other reagent (O₂). Once we determine the mass of O₂ that reacted, we subtract that from the original amount to determine the amount left over. According to the mass-mass calculation,

Because we reacted 16.0 g of our original O₂, we subtract that from the original amount, 50.0 g, to get the mass of O₂ remaining:

You must remember to perform this final subtraction to determine the amount remaining; a common error is to report the 16.0 g as the amount remaining.

As you learned in chapter 3, density is the mass per unit volume of a substance. If we are given the density of a substance, we can use it in stoichiometric calculations involving liquid reactants and/or products, as Example 10.2-2 demonstrates.

Example 10.2-2

Ethyl acetate (CH₃CO₂C₂H₅) is the solvent in many fingernail polish removers and is used to decaffeinate coffee beans and tea leaves. It is prepared by reacting ethanol (C₂H₅OH) with acetic acid (CH₃CO₂H); the other product is water. A small amount of sulfuric acid is used to accelerate the reaction, but the sulfuric acid is not consumed and does not appear in the balanced chemical equation. Given 10.0 mL each of acetic acid and ethanol, how many grams of ethyl acetate can be prepared from this reaction? The densities of acetic acid and ethanol are 1.0492 g/mL and 0.7893 g/mL, respectively.

Given: reactants, products, and volumes and densities of reactants

Asked for: mass of product

Strategy:

A Balance the chemical equation for the reaction.

B Use the given densities to convert from volume to mass. Then use each molar mass to convert from mass to moles.

C Using mole ratios, determine which substance is the limiting reactant. After identifying the limiting reactant, use mole ratios based on the number of moles of limiting reactant to determine the number of moles of product.

D Convert from moles of product to mass of product.

Solution:

A We always begin by writing the balanced chemical equation for the reaction:

C₂H₅OH(l) + CH₃CO₂H(aq) → CH₃CO₂C₂H₅(aq) + H₂O(l)

B We need to calculate the number of moles of ethanol and acetic acid that are present in 10.0 mL of each. Recall from that the density of a substance is the mass divided by the volume:

$$\text{density}=\frac{\text{mass}}{\text{volume}}$$

Rearranging this expression gives mass = (density)(volume). We can replace mass by the product of the density and the volume to calculate the number of moles of each substance in 10.0 mL (remember, 1 mL = 1 cm³):

$$\begin{array}{ll}{\text{moles C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}\hfill & =\frac{{\text{mass C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}{{\text{molar mass C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}\hfill \\ \hfill & =\frac{{\text{volume C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}\times {\text{density C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}{{\text{molar mass C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}\hfill \\ \hfill & =\text{10}\text{.0}\cancel{{\text{mL C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}\times \frac{\text{0}\text{.7893}\cancel{{\text{g C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}}{\text{1}\cancel{{\text{mL C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}}\times \frac{1{\text{mol C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}{\text{46}\text{.07}\cancel{{\text{g C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}}\hfill \\ \hfill & =\text{0}{\text{.171 mol C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}\hfill \\ {\text{moles CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}\hfill & =\frac{{\text{mass CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}{{\text{molar mass CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}\hfill \\ \hfill & =\frac{{\text{volume CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}\times {\text{density CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}{{\text{molar mass CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}\hfill \\ \hfill & =\text{10}\text{.0}\cancel{{\text{mL CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}\times \frac{\text{1}\text{.0492}\cancel{{\text{g CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}}{\text{1}\cancel{{\text{mL CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}}\times \frac{1{\text{mol CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}{\text{60}\text{.05}\cancel{{\text{g CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}}}\hfill \\ \hfill & =\text{0}{\text{.175 mol CH}}_{\text{3}}{\text{CO}}_{\text{2}}\text{H}\hfill \end{array}$$

C The number of moles of acetic acid exceeds the number of moles of ethanol. Because the reactants both have coefficients of 1 in the balanced chemical equation, the mole ratio is 1:1. We have 0.171 mol of ethanol and 0.175 mol of acetic acid, so ethanol is the limiting reactant and acetic acid is in excess. The coefficient in the balanced chemical equation for the product (ethyl acetate) is also 1, so the mole ratio of ethanol and ethyl acetate is also 1:1. This means that given 0.171 mol of ethanol, the amount of ethyl acetate produced must also be 0.171 mol:

$$\begin{array}{ll}\text{moles ethyl acetate}\hfill & =\text{mol ethanol}\times \frac{\text{1 mol ethyl acetate}}{\text{1 mol ethanol}}\hfill \\ \hfill & =\text{0}\text{.171}\cancel{{\text{mol C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}\times \frac{{\text{1 mol CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}{\text{1}\cancel{{\text{mol C}}_{\text{2}}{\text{H}}_{\text{5}}\text{OH}}}\hfill \\ \hfill & =\text{0}{\text{.171 mol CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}\hfill \end{array}$$

D The final step is to determine the mass of ethyl acetate that can be formed, which we do by multiplying the number of moles by the molar mass:

$$\begin{array}{ll}\text{mass of ethyl acetate}\hfill & =\text{mol ethyl acetate}\times \text{molar mass ethyl acetate}\hfill \\ \hfill & =\text{0}\text{.171}\cancel{{\text{mol CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}\times \frac{\text{88}{\text{.11 g CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}{\text{1}\cancel{{\text{mol CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}}\hfill \\ \hfill & =\text{15}{\text{.1 g CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}\hfill \end{array}$$

Thus 15.1 g of ethyl acetate can be prepared in this reaction. If necessary, you could use the density of ethyl acetate (0.9003 g/cm³) to determine the volume of ethyl acetate that could be produced:

$$\begin{array}{ll}\text{volume of ethyl acetate}\hfill & =\text{15}\text{.1}\cancel{{\text{g CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}\times \frac{{\text{1 mL CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}{\text{0}\text{.9003}\cancel{{\text{g CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}}}\hfill \\ \hfill & =\text{16}{\text{.8 mL CH}}_{\text{3}}{\text{CO}}_{\text{2}}{\text{C}}_{\text{2}}{\text{H}}_{\text{5}}\hfill \end{array}$$

Exercise

Under appropriate conditions, the reaction of elemental phosphorus and elemental sulfur produces the compound P₄S₁₀. How much P₄S₁₀ can be prepared starting with 10.0 g of P₄ and 30.0 g of S₈?

Answer: 35.9 g