This is "Week 1", section 1.2 from the book 32 Weeks of OChem (v. 1.0).
1.2 How do we know?
Learning Objectives
- To be able to identify the molecular ion and its isotopic peak from a mass spectrum.
- To be able to calculate a molecular formula from a mass spectrum.
- To be able to deduce the degree of unsaturation using the rings + double bonds formula.
- To associate infrared stretching frequencies with bond strength and the mass of the bonded atoms.
- To learn characteristic stretching and bending frequencies in an infrared spectrum of a hydrocarbon.
- To use the information revealed in DEPT, Off-resonance proton decoupled, and Broad band decoupled 13C NMR experiments.
- To use chemical shift, integration and splitting information from a 1H NMR experiment.
Atoms are too small to see. For that matter collections of thousands of atoms are still too small to see. So, how do we know what atoms are present in a compound and how do we know the connectedness of those atoms? There are several tools of the trade chemists can employ. Most typically a chemist has access to an infrared spectrum (IR), a mass spectrum (MS), a nuclear magnetic resonance spectrum (NMR). In many organic chemistry textbooks spectroscopy is set aside in two or three separate chapters somewhere in the middle of the textbook. In this course we are glossing over the physics, some of which isn't necessary to totally understand, and diving head first into the interpetration of the spectra. The physics is interesting; however, at this stage of the game, we can have a whole lot of fun and learn a tremendous amount about these compounds just by charging straight to the spectra. You should not expect any one week's worth of ".2" sections in this supplement to be a complete story for any experimental technique. The only goal of these sections is to give you enough information to enable you to do the week's problems. Each week we will kick up the complexity for each of the three spectra. Stick with these ".2" sections and by the end of 32 weeks, you can be among the best prepared undergraduate students in the world with respect to spectroscopic determination of organic structures. Take little steps and make them FUN!
In the interpretation of spectra, you will run into a lot of "maybes." In practice one experiment rarely unequivicobly
MS
Figure 1.2-1 A Mass Spectrometer

The 1 MV accelerator mass spectrometer at Lawrence Livermore National Laboratory http://bioams.llnl.gov/equipment.php 14C and tritium analyses of biomedical samples submitted by Resource users are conducted using this 1 MV system. The AMS spectrometer consists of a cesium sputter source, low-energy injection beam line, the high voltage collision cell (accelerator), a high-energy mass spectrometer and a particle detector for energy measurements (proceeding clockwise from lower left in the photograph).This image is a work of a United States Department of Energy (or predecessor organization) employee, taken or made as part of that person's official duties. As a work of the U.S. federal government, the image is in the public domain via Wikimedia Commons.
Simply put, a mass spectrum is a graph showing the masses and abundances of all the ions that result when you smash a molecule with a hammer. There are lots of places to read about the scales used to weigh the ions and the hammers used to smash the molecules but that discussion is left to others. Remember, we're cutting right to the chase and learning how to elucidate structures from spectra.
Oftentimes, but not always, and maybe not even usually, it's possible to get a molecular formula from the mass spectrum. One quick and dirty approach is to look at the highest mass region of the spectrum with the hopes of spotting what is called the peak group for the molecular ion, M+. For this quick and dirty trick to work you need to identify a pair of peaks in the M+. The taller and lighter mass peak is called the "base peak" and is from the M+ ion where all of the carbons are 12C. The peak next door is called the (M+1)+, or "isotopic peak." This isotopic peak comes from an ion which has one 13C instead of a 12C as in the base peak. . This peak is called the M+1 isotopic peak. Nature has endowed the earth with 1.1 13C atoms for every 100 C atoms. With this knowledge we can do some arithmetic.
- Normalize the base peak; i.e., multiply it's intensity by some number to make it 100.
- Multiply the intensity of the isotopic peak by this same normalization factor you applied to the base peak. This is called the "normalized isotopic peak" intensity.
- Divide the normalized isotopic peak's intensity by 1.1. This is the approximate number of carbons in the compound which must of course be an integer.
- Take the difference between the mass of the base peak and the number of carbons × 12. This is the number of hydrogens.
This quick and dirty approach will work 100% of the time for the spectra in our first several weeks of problems. But keep in mind, this is still tee-ball.
If you know the molecular formula, then you can calculate the number of rings + π bonds.
Equation 1.2-1 Rings + Double Bonds formula (aka, Degree of Unsaturation or Index of Hydrogen Deficiency)
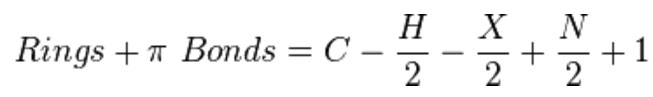
Credit: https://en.wikipedia.org/wiki/Degree_of_unsaturation
Where C = number of carbons, H = number of hydrogens, X= number of halogens and N = number of nitrogens. Divalent atoms like oxygen never contribute a term to this R + DB equation. It's easier to remember in words. Take the number of C atoms, subtract half the number of monovalent atoms, skip the divalent atoms, add half the number of trivalent atoms and then add 1. Remember, a hydrocarbon that has no rings or double bonds has 2n + 2 hydrogen atoms.
IR
Figure 1.2-1 A Fourier Transform Infrared Spectrophotometer (FTIR)

(Left) An FTIR with the sample chamber open. (Right) The same instrument with the housing off. An inner liner has also been removed which protects the KBr optics from moisture. .By Kkmurray (Own work) [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0) or GFDL (http://www.gnu.org/copyleft/fdl.html)], via Wikimedia Commons
A large amount of interpretation of an IR is qualitative but there are also a lot of numbers to memorize; however, do NOT memorize table 1.2-1 (below).
Table 1.2-1 Average Bond Energies (kJ/mol) adapted from http://chemwiki.ucdavis.edu/Core/Theoretical_Chemistry/Chemical_Bonding/General_Principles_of_Chemical_Bonding/Bond_Energies
| Single Bonds | Multiple Bonds | ||||||
| C—H |
413
|
N—H |
391
|
C = C |
614
|
||
| C—C |
347
|
C ≡ C |
839
|
||||
| C—N |
305
|
|
C = O* |
745
|
|||
| C—O |
358
|
S—H |
347
|
||||
| C—F |
485
|
N = O |
607
|
||||
| C—Cl |
339
|
O—H |
467
|
||||
| C—Br |
276
|
||||||
| C—I |
240
|
C ≡ N |
891
|
||||
| C—S |
259
|
|
C = N |
615
|
|||
|
*C == O(CO2) = 799
|
|||||||
The take home message is that different bonds have different energies. For IR we often use the analogy that the atoms connected by a bond are like masses on a spring. Looking at the table above, we can see a single bond is lower energy than a double bond which is lower energy than a triple bond. The spring analogy says the spring gets stiffer as we go from a single bond to a triple bond. Continuing the analogy, the stretching frequency of a heavy mass attached to a spring is slower than the stretching frequency for a spring attached to a lighter mass. This difference in frequency associated with different mass matches the observations from Table 1.2-1. The reason for introducing this bit of theory is that it helps one remember the relative region of stretching frequencies in an IR spectrum.
The IR experiment is vibrational, meaning the bonds are made to bend and stretch with the IR energy. Table 1.2-1 helps you rank the IR absorption frequency. The intensity of the absorption is proportional to the change in dipole moment. When the dipole moment does not change during a vibration, it is IR silent. Big dipole moment changes mean big absorption intensities.
Table 1.2-2 Typical Absorption Frequencies adapted from http://chemwiki.ucdavis.edu/Core/Organic_Chemistry/Spectroscopy/Infrared_Spectroscopy
Stretching Vibrations |
Bending Vibrations |
|||||
|---|---|---|---|---|---|---|
Functional Class |
Range (cm-1) |
Intensity |
Assignment |
Range (cm-1) |
Intensity |
Assignment |
Alkanes |
2850-3000 | str | CH3, CH2
& CH 2 or 3 bands |
1350-1470 1370-1390 720-725 |
med med wk |
CH2 & CH3
deformation CH3 deformation CH2 rocking |
Alkenes |
3020-3100 1630-1680 1900-2000 |
med var str |
=C-H & =CH2 (usually sharp) C=C (symmetry reduces intensity) C=C asymmetric stretch |
880-995 780-850 675-730 |
str med med |
=C-H & =CH2 (out-of-plane bending) cis-RCH=CHR |
Alkynes |
3300 2100-2250 |
str var |
C-H (usually sharp) C≡C (symmetry reduces intensity) |
600-700 | str | ≡C-H deformation |
There is a lot of information in table 1.2-2. The five points below need to be memorized from this table this week.
From the stretches-
- The C-H stretch in an alkane is below 3000 cm-1. The =C-H stretch of an alkene is pointy and between 3000 and 3300 cm-1. The ≡C-H stretch of an alkyne is pointy and above 3300 cm-1.
- The C=C bond stretch appears between 1630 and 1680 cm-1. Another C=C bond stretch appears between 1900 and 2000 cm-1.
- The C≡C bond stretch is between 2100 and 2250 cm-1.
From the bends-
The business from 1350 to 1470 cm-1 can reveal alkyl groups and deserves some attention.
- A doublet of two identical peaks centered around 1370 cm-1 indicates an isopropyl group. A doublet where one peak is larger than the other in this region indicates a t-butyl group.
- A peak at 1450 cm-1 indicates a -CH2- (methylene) group. A peak at 1375 cm-1 indicates a -CH3 (methyl) group.
NMR
Figure 1.2-3 An NMR

By Mike25 (Own work) [Public domain], via Wikimedia Commons
The NMR experiment distinguishes nuclei in molecules and gives a glimpse of their nuclear environment. Without getting into the quantum mechanics, suffice it to say that some nuclei are susceptible to having their spin flipped while other nuclei are not. It's this spin flipping that gives a signal in our NMR spectra. In this course we'll be flipping 13C nuclei and 1H nuclei.
13C-NMR
We will use three types of 13C experiments for our spectra in this course.
- Distortionless Enhancement of Polarization Transfer (DEPT)
- Off-Resonance Proton Decoupled
- Broad Band Proton Decoupled
Again, employing our modus operandi, we're skipping the physics and going straight to what these three different experiments tell us.
DEPT: Great for finding CH2's and >C<
- Quaternary carbons, those connected to no hydrogens, give no signal.
- A methylene carbon, one connected to 2 hydrogens, gives an upside-down singlet.
- A methyl carbon, which is one connected to 3 hydrogens, and methine carbon, which is one connected to 1 hydrogen, give ordinary singlet peaks.
Off-Resonance Proton Decoupled: Gives a signal split into one more peak than the number of hydrogens attached.
- quartet is a CH3
- triplet is a CH2
- doublet is a CH
- singlet is a C (no hydrogens)
Broad Band Proton Decoupled: Great for counting equivalent carbons. Each carbon gives a singlet.
The placement of the signal on horizontal scale on the spectrum is called the chemical shift. This is a relative scale comparing the signal to that from a reference compound. The chemical shift is the same for all three 13C experiments. Typical 13C chemical shifts are shown below in Table 1.2-3.
Table 1.2-3 Some 13C chemical shifts adapted from http://chemwiki.ucdavis.edu/Core/Physical_Chemistry/Spectroscopy/Magnetic_Resonance_Spectroscopies/Nuclear_Magnetic_Resonance/NMR%3A_Experimental/NMR%3A_Interpretation

1H NMR
This technique uses the same instrument as shown in figure 1.1-3. Historically, the 1H-NMR experiment came first; however, extracting structural information from 1H-NMR spectra can be a little more complicated than it is from the 13C-NMR data. We'll only consider one 1H-NMR experiment. Again, chemical shift, i.e., the position of the peaks on the horizontal axis is very informative. There are two other important bits of information we can get from a 1H-NMR that are not considered for 13C-NMR. The area under the peaks can be integrated to quantify the number of hydrogens. This is called "integration." Also, the signals are split by the protons on neighboring carbon atoms. This is called "signal splitting pattern" So that's three pieces of information we need to extract from our 1H NMR spectra-
- chemical shift
- integration
- signal splitting pattern
Chemical Shift
Table 1.2-4 Some 1H chemical shifts adapted from http://chemwiki.ucdavis.edu/Core/Physical_Chemistry/Spectroscopy/Magnetic_Resonance_Spectroscopies/Nuclear_Magnetic_Resonance/NMR%3A_Experimental/NMR%3A_Interpretation

Integration
The area of the curve under each peak is often displayed as a line plotted above the spectrum. The height from one plateau to another gives the relative number of equivalent protons moving from left to right across the spectrum. Rather than an integration line, sometimes the number of protons is displayed above the peak group. The least convenient approach to integration is to require the viewer to estimate area based on the intensity of the peaks. Many of the spectra for this course will require this least convenient approach.
Signal Splitting Pattern
The hydrogens on carbons adjacent to the carbon with the hydrogens giving the signal will split the signal into a multiplet. This is called "spin-spin coupling." Signals are split according to the n+1 rule. The number of peaks in the multiplet is proportional to the number of hydrogens on the adjacent carbons plus 1. So if carbon "A" has 3 hydrogens and carbon "B" has 1 hydrogen. The signal from the protons on carbon "A" will be split into a doublet. The signal from the proton on carbon "B" will be split into a quartet. The intensities of the peaks in the multiplet will be in the ratio given by Pascal's triangle as shown below:
Figure 1.2-4 Pascal's Triangle
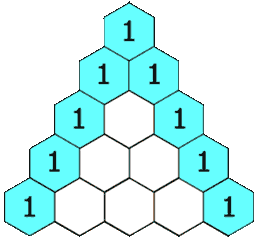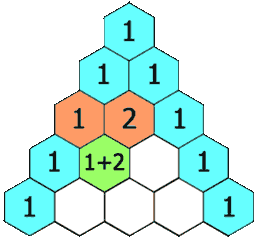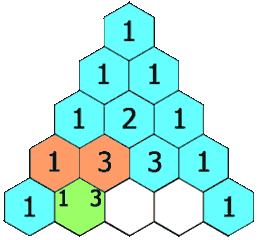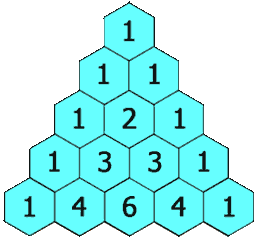
Image Credit: By Hersfold on the English Wikipedia (Own work) [Public domain], via Wikimedia Commons
So using the above example, the doublet will appear as a 1:1 split. The quartet for the protons on carbon "B" will appear as a 1:4:4:1 split.




