Gas Laws

11.3 Gas Laws

Learning Objective

To understand the relationships among pressure, temperature, volume, and the amount of a gas.

Early scientists explored the relationships among the pressure of a gas (P) and its temperature (T), volume (V), and amount (n) by holding two of the four variables constant (amount and temperature, for example), varying a third (such as pressure), and measuring the effect of the change on the fourth (in this case, volume). The history of their discoveries provides several excellent examples of the scientific method as presented in Section 1.1".

The Relationship between Pressure and Volume

As the pressure on a gas increases, the volume of the gas decreases because the gas particles are forced closer together. Conversely, as the pressure on a gas decreases, the gas volume increases because the gas particles can now move farther apart. Weather balloons get larger as they rise through the atmosphere to regions of lower pressure because the volume of the gas has increased; that is, the atmospheric gas exerts less pressure on the surface of the balloon, so the interior gas expands until the internal and external pressures are equal.

Robert Boyle (1627–1691)

Boyle, the youngest (and 14th!) child of the Earl of Cork, was an important early figure in chemistry whose views were often at odds with accepted wisdom. Boyle’s studies of gases are reported to have utilized a very tall J-tube that he set up in the entryway of his house, which was several stories tall. He is known for the gas law that bears his name and for his book, The Sceptical Chymist, which was published in 1661 and influenced chemists for many years after his death. In addition, one of Boyle’s early essays on morals is said to have inspired Jonathan Swift to write Gulliver’s Travels.

The Irish chemist Robert Boyle (1627–1691) carried out some of the earliest experiments that determined the quantitative relationship between the pressure and the volume of a gas. Boyle used a J-shaped tube partially filled with mercury, as shown in Figure 11.3(a) . In these experiments, a small amount of a gas or air is trapped above the mercury column, and its volume is measured at atmospheric pressure and constant temperature. More mercury is then poured into the open arm to increase the pressure on the gas sample. The pressure on the gas is atmospheric pressure plus the difference in the heights of the mercury columns, and the resulting volume is measured. This process is repeated until either there is no more room in the open arm or the volume of the gas is too small to be measured accurately. Data such as those from one of Boyle’s own experiments may be plotted in several ways (Figure 11.3(b) ). A simple plot of V versus P gives a curve called a hyperbola and reveals an inverse relationship between pressure and volume: as the pressure is doubled, the volume decreases by a factor of two. This relationship between the two quantities is described as follows:

Equation 11.3(eq1)

PV = constant

Figure 11.3(a) Boyle’s Experiment Using a J-Shaped Tube to Determine the Relationship between Gas Pressure and Volume

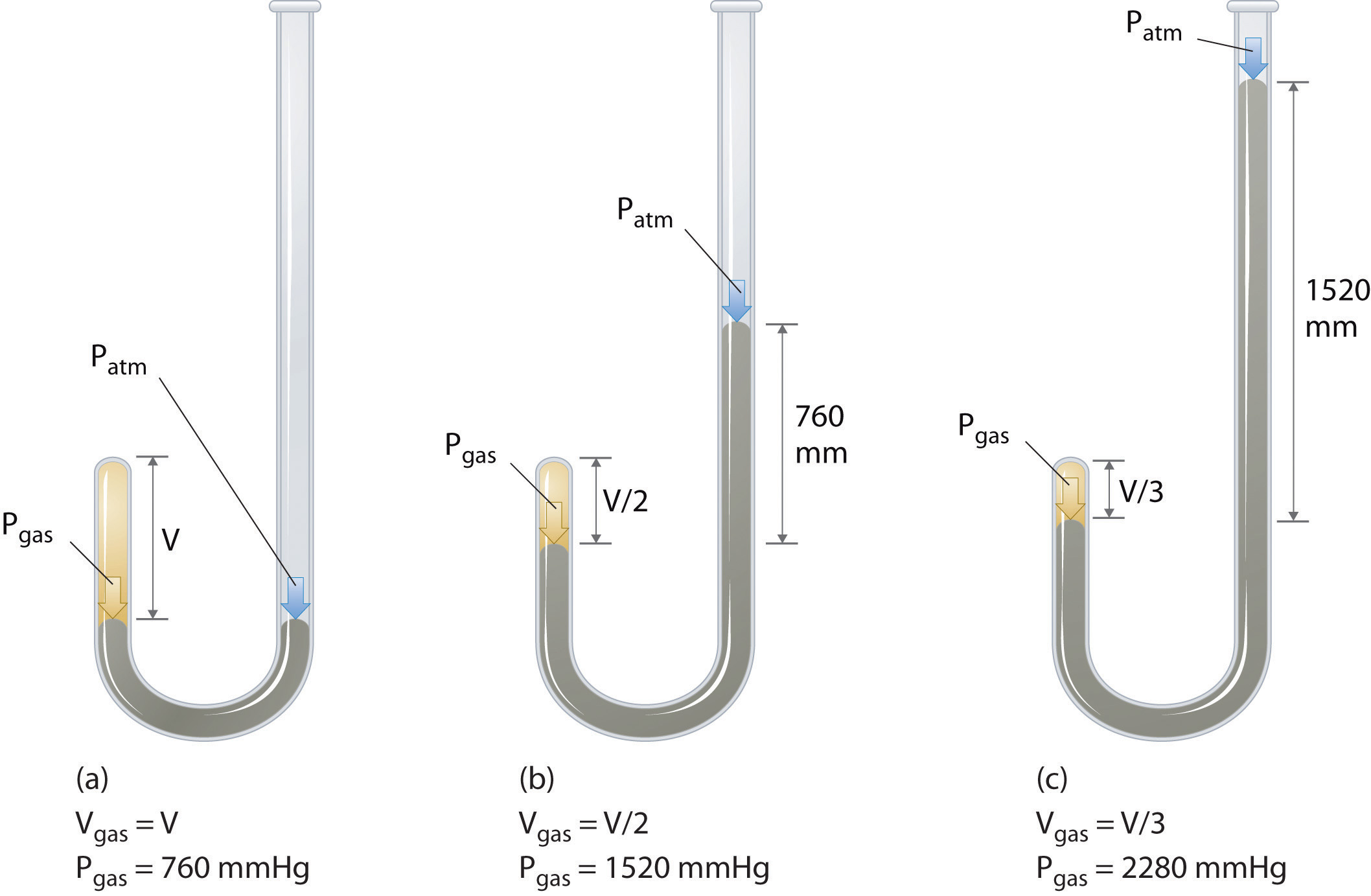
(a) Initially the gas is at a pressure of 1 atm = 760 mmHg (the mercury is at the same height in both the arm containing the sample and the arm open to the atmosphere); its volume is V. (b) If enough mercury is added to the right side to give a difference in height of 760 mmHg between the two arms, the pressure of the gas is 760 mmHg (atmospheric pressure) + 760 mmHg = 1520 mmHg and the volume is V/2. (c) If an additional 760 mmHg is added to the column on the right, the total pressure on the gas increases to 2280 mmHg, and the volume of the gas decreases to V/3.

Figure 11.3(b) Plots of Boyle’s Data

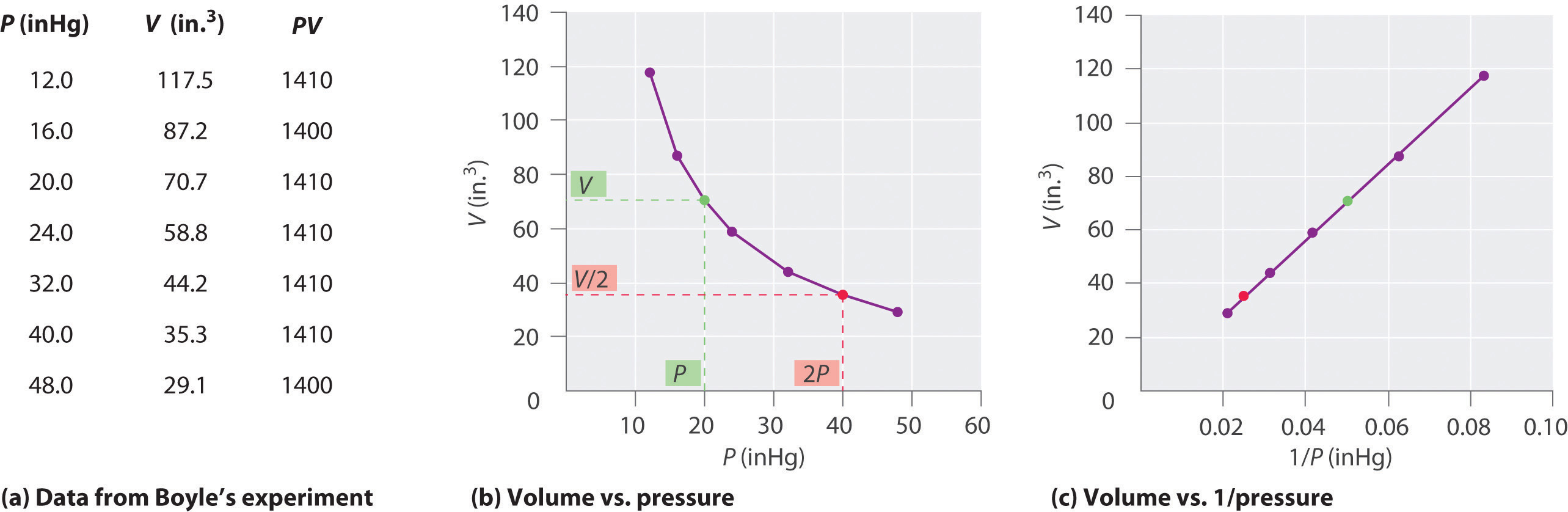
(a) Here are actual data from a typical experiment conducted by Boyle. Boyle used non-SI units to measure the volume (in.³ rather than cm³) and the pressure (in. Hg rather than mmHg). (b) This plot of pressure versus volume is a hyperbola. Because PV is a constant, decreasing the pressure by a factor of two results in a twofold increase in volume and vice versa. (c) A plot of volume versus 1/pressure for the same data shows the inverse linear relationship between the two quantities, as expressed by the equation V = constant/P.

Dividing both sides by P gives an equation illustrating the inverse relationship between P and V:

Equation 11.3(eq2)

V = \frac{constant}{P} = constant (\frac{1}{P}) or V \propto \frac{1}{P}

where the ∝ symbol is read “is proportional to.” A plot of V versus 1/P is thus a straight line whose slope is equal to the constant in Equation 11.3(eq1) and Equation 11.3(eq2). Dividing both sides of Equation 11.3(eq1) by V instead of P gives a similar relationship between P and 1/V. The numerical value of the constant depends on the amount of gas used in the experiment and on the temperature at which the experiments are carried out. This relationship between pressure and volume is known as Boyle’s lawA law that states that at constant temperature, the volume of a fixed amount of a gas is inversely proportional to its pressure., after its discoverer, and can be stated as follows: At constant temperature, the volume of a fixed amount of a gas is inversely proportional to its pressure.

Example 11.3-1

A sample of gas occupies a volume of 35 mL at a pressure of 1.2 atm. What volume, in mL, would the sample need to occupy in order for the pressure to be increased to 2.2 atm, at constant temperature?

Given: volume at an initial pressure.

Asked for: volume at a different pressure.

Strategy:

Use Boyle's Law to create a "pressure factor" (not really a conversion factor) for the new condition.

Solution:

Create a table of values from the problem.

V₁ = 35 mL	V₂ = ?
P₁ = 1.2 atm	P₂ = 2.2 atm

From Boyle's Law, since the pressure is increasing, the volume must be decreasing. Therefore the pressure factor must be less than one. In other words, the smaller pressure must go on top of the bigger pressure; otherwise the pressure factor would be more than one.

V_{2} = (35 mL) (\frac{1.2 atm}{2.2 atm}) = 19 mL

Note that units of pressure in the numerator and denominator must be the same (if they were given in different units one must be corrected to make them the same. This also points out the importance of including units, even though these are not conversion factors.

Exercise

A sample of gas occupies a volume of 0.45 L at 740 torr pressure, and 25°C. Calculate the new pressure, in torr, if the volume is changed to 0.94 L at constant temperature.

Answer: 354 torr

The Relationship between Temperature and Volume

Hot air rises, which is why hot-air balloons ascend through the atmosphere and why warm air collects near the ceiling and cooler air collects at ground level. Because of this behavior, heating registers are placed on or near the floor, and vents for air-conditioning are placed on or near the ceiling. The fundamental reason for this behavior is that gases expand when they are heated. Because the same amount of substance now occupies a greater volume, hot air is less dense than cold air. The substance with the lower density—in this case hot air—rises through the substance with the higher density, the cooler air.

The first experiments to quantify the relationship between the temperature and the volume of a gas were carried out in 1783 by an avid balloonist, the French chemist Jacques Alexandre César Charles (1746–1823). Charles’s initial experiments showed that a plot of the volume of a given sample of gas versus temperature (in degrees Celsius) at constant pressure is a straight line. Similar but more precise studies were carried out by another balloon enthusiast, the Frenchman Joseph-Louis Gay-Lussac (1778–1850), who showed that a plot of V versus T was a straight line that could be extrapolated to a point at zero volume, a theoretical condition now known to correspond to −273.15°C (Figure 11.3(c) ).A sample of gas cannot really have a volume of zero because any sample of matter must have some volume. Furthermore, at 1 atm pressure all gases liquefy at temperatures well above −273.15°C. Note from part (a) in Figure 11.3(c) that the slope of the plot of V versus T varies for the same gas at different pressures but that the intercept remains constant at −273.15°C. Similarly, as shown in part (b) in Figure 11.3(c) , plots of V versus T for different amounts of varied gases are straight lines with different slopes but the same intercept on the T axis.

Jacques Alexandre César Charles (1746–1823) and Joseph-Louis Gay-Lussac (1778–1850)

In 1783, Charles filled a balloon (“aerostatic globe”) with hydrogen (generated by the reaction of iron with more than 200 kg of acid over several days) and flew successfully for almost an hour. When the balloon descended in a nearby village, however, the terrified townspeople destroyed it. In 1804, Gay-Lussac managed to ascend to 23,000 ft (more than 7000 m) to collect samples of the atmosphere to analyze its composition as a function of altitude. In the process, he had trouble breathing and nearly froze to death, but he set an altitude record that endured for decades. (To put Gay-Lussac’s achievement in perspective, recall that modern jetliners cruise at only 35,000 ft!)

The significance of the invariant T intercept in plots of V versus T was recognized in 1848 by the British physicist William Thomson (1824–1907), later named Lord Kelvin. He postulated that −273.15°C was the lowest possible temperature that could theoretically be achieved, for which he coined the term absolute zero (0 K)The lowest possible temperature that can be theoretically achieved; it corresponds to −273.15°C..

We can state Charles’s and Gay-Lussac’s findings in simple terms: At constant pressure, the volume of a fixed amount of gas is directly proportional to its absolute temperature (in kelvins). This relationship, illustrated in part (b) in Figure 11.3(c) , is often referred to as Charles’s lawA law that states that at constant pressure, the volume of a fixed amount of gas is directly proportional to its absolute temperature (in kelvins). and is stated mathematically as

Equation 11.3(eq3)

V = (constant) [T (in K)] or V \propto T (in K, at constant P)

Charles’s law is valid for virtually all gases at temperatures well above their boiling points. Note that the temperature must be expressed in kelvins, not in degrees Celsius.

Figure 11.3(c) The Relationship between Volume and Temperature

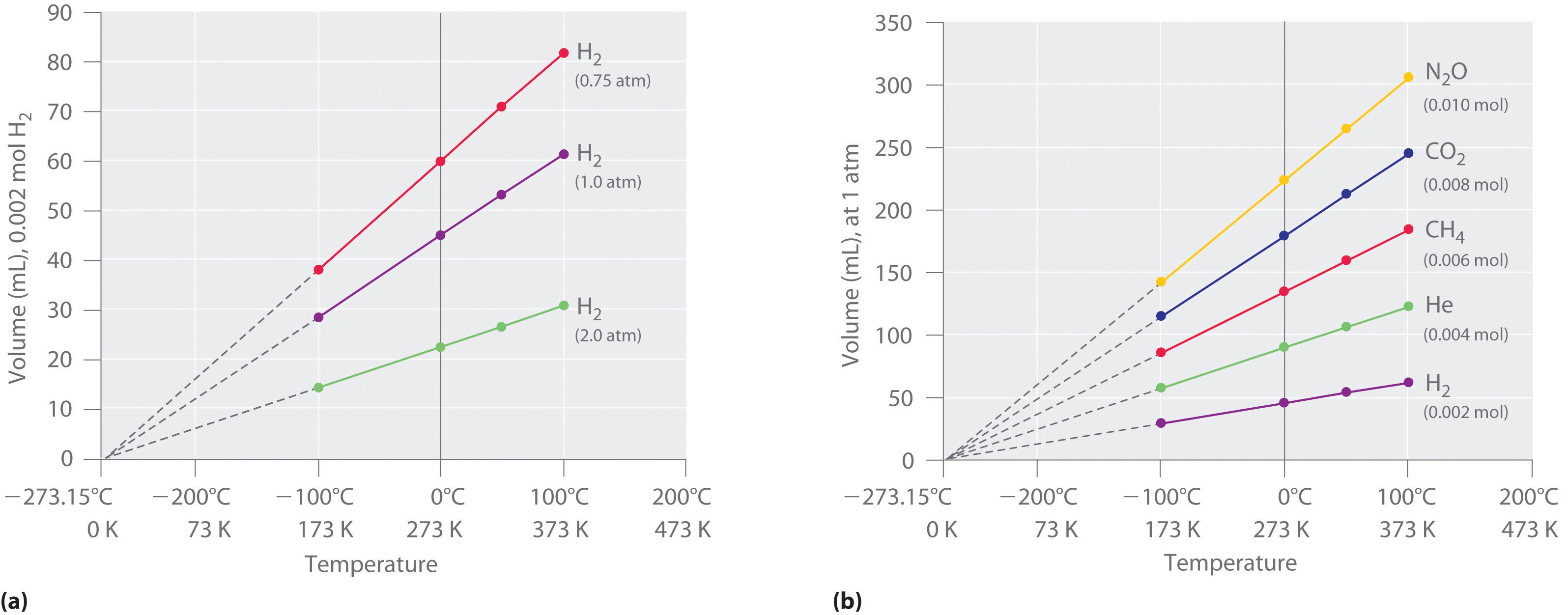
(a) In these plots of volume versus temperature for equal-sized samples of H₂ at three different pressures, the solid lines show the experimentally measured data down to −100°C, and the broken lines show the extrapolation of the data to V = 0. The temperature scale is given in both degrees Celsius and kelvins. Although the slopes of the lines decrease with increasing pressure, all of the lines extrapolate to the same temperature at V = 0 (−273.15°C = 0 K). (b) In these plots of volume versus temperature for different amounts of selected gases at 1 atm pressure, all the plots extrapolate to a value of V = 0 at −273.15°C, regardless of the identity or the amount of the gas.

Example 11.3-2

A sample of gas occupies a volume of 2.5 liters at 20 °C. What volume would it occupy at 100 °C, assuming that the pressure remains constant?

Given: volume at an initial temperature.

Asked for: volume at a different temperature.

Strategy:

Use Charles's Law to create a "temperature factor" (not really a conversion factor) for the new condition.

Solution:

Create a table of values from the problem.

V₁ = 2.5 L	V₂ = ?
T₁ = 20°C = 293 K	T₂ = 100°C = 373 K

To find the new volume we multiply the original times some temperature factor. To determine this temperature factor we look at the change in the temperature (in K), and decide how this will affect the volume. In this case the temperature is increasing, so we know that the volume must increase, (if the pressure is to remain constant). Therefore, the temperature factor is written as 373K / 293K(that is, a fraction larger than one). We can thus calculate the new volume to be

V_{2} = (2.5 L) (\frac{373 K}{293 K}) = 3.2 L

Exercise

A sample of gas, at constant pressure, occupies a volume of 2.50 L at at 150°C. Calculate the new volume, in mL, if the temperature becomes 135°C.

Answer: 2410 mL

Example 11.3-3

A sample of gas occupies a volume of 1.8 liters at 150°C. What temperature, in °C, would this need to be changed to in order to give a volume of 2.2 liters, at constant pressure?

Given: temperature at an initial volume.

Asked for: temperature at a different volume.

Strategy:

Use Charles's Law to create a "volume factor" (not really a conversion factor) for the new condition.

Solution:

Create a table of values from the problem.

V₁ = 1.8 L	V₂ = 2.2 L
T₁ = 150°C = 423 K	T₂ = ?

Since the volume is increasing, the temperature must also be increasing (to keep the pressure constant). Therefore the volume factor must be greater than one, or 2.2 L / 1.8L.

T_{2} = (423 K) (\frac{2.2 L}{1.8 L}) = 517 K

Remember that this must be calculated in K, since volume and temperature are only directly proportional if the temperature is measured on the absolute (Kelvin) scale. Then to find this temperature in °C, we must subtract 273, to give

517 - 273 = 244°C.

Exercise

A sample of gas, at constant pressure, occupies a volume of 2.50 L at at 150°C. Calculate the new temperature, in °C, if the volume is changed to 2.60 L and the pressure remains constant.

Answer: 167 °C

The Relationship between Temperature and Pressure

If a gas is heated in a closed container, the pressure will increase, due to increased kinetic energy of the molecules. If the temperature is measured on the Kelvin (absolute) scale, it is found that pressure is directly proportional to temperature. This is known as Gay-Lussac's Law. That is, if the temperature (on the Kelvin scale) is doubled, the pressure will be twice as great, and if the temperature is changed to one-half of what it originally was, the pressure will be one-half as great, assuming that the volume remains constant. This relationship is stated as follows: Pressure is directly proportional to the absolute (Kelvin) temperature, at constant volume. This can be stated mathematically as,

P = kT

where k is a constant. We can rearrange this to give

Equation 11.3(eq4)

\frac{P}{T} = k

which means that the pressure divided by the absolute temperature is a constant. Thus if the temperature is doubled (on the Kelvin scale) the pressure must also double, in order for P/T to be constant.

Example 11.3-4

A sample of gas at a temperature of 100 °C exerts a pressure of 800 mm Hg. Calculate the new pressure, in mm Hg, if the temperature is decreased to 80 °C, assuming that the volume remains constant.

Given: pressure at an initial temperature.

Asked for: pressure at a different temperature.

Strategy:

Use Gay-Lussac's Law to create a "temperature factor" (not really a conversion factor) for the new condition.

Solution:

Create a table of values from the problem.

P₁ = 800 mm Hg	P₂ = ?
T₁ = 100°C = 373 K	T₂ = 800°C = 353 K

To find the new pressure we multiply the original pressure times some temperature factor. To determine this temperature factor we look at the change in the temperature (in K), and decide how this will affect the pressure. In this case the temperature is decreasing, so we know that the pressure must decrease. Therefore the temperature factor must be less than on (keep in mind that all temperatures must be in K), and thus the factor used is 353K / 373K. Using this, the new pressure is calculated as follows.

P_{2} = (800 mm Hg) (\frac{353 K}{373 K}) = 757 mm Hg

Exercise

A sample of gas, at constant volume, exerts a pressure of 720 mm Hg at at 100°C. What would the pressure be, in mm Hg, if the temperature is increased to 200°C.

Answer: 913 mm Hg

Example 11.3-5

A sample of gas at 100 °C exerts a pressure of 800 torr. What would the temperature need to be changed to, in °C, in order for the pressure to become 400 torr, if the volume remains constant?

Given: temperature at an initial pressure.

Asked for: temperature at a different pressure.

Strategy:

Use Gay-Lussac's Law to create a "pressure factor" (not really a conversion factor) for the new condition.

Solution:

Create a table of values from the problem.

P₁ = 800 torr	P₂ = 400 torr
T₁ = 100°C = 373 K	T₂ = ?

Since the pressure is decreasing, the temperature must decrease. Thus the factor used must be less than one. The new temperature, in K, is calculated as follows.

T_{2} = (373 K) (\frac{400 torr}{800 torr}) = 186.5 K

186.5 - 273 = -86.5°C.

Notice that the temperature on the absolute (Kelvin) scale is half of what it was originally, but this is not true on the Celsius scale.

Exercise

A sample of gas occupies a volume of 4.2 L at a temperature of o 23°C and a pressure of 0.85 atm. Calculate the presure, in atm, if the temperature is changed to 48 °C, at constant volume.

Answer: 0.92 atm

Calculations Involving Two Changes - Combined Gas Law

Gas law calculation involving two changes, such as temperature and pressure, are done in the same way as the previous examples, but each change is considered individually. That is, we first consider how the volume would change with the given change in temperature, and then consider how this new volume would change with the new pressure. The calculation is set up as one problem. Consider the following example.

Example 11.3-6

A sample of gas occupies a volume of 2.6 liters at a pressure of 700 mm Hg and a temperature of 100 °C. Calculate the volume of the gas at STP. (STP = 1 atm, 0 °C.)

Given: volume at an initial temperature and pressure.

Asked for: volume at a different temperature and a different pressure.

Strategy:

Employ Boyle's Law to create a pressure factor and employ Charles's Law to create a temperature factor.

Solution:

Create a table of values from the problem.

V₁ = 2.6 L	V₂ = ?
T₁ = 100°C = 373 K	T₂ = 0°C = 273 K
P₁ = 700 mm Hg	P₂ = 760 mm Hg

We set up the problem in the same way as was done in previous examples, considering each change individually. That is, since the temperature is decreasing the volume will decrease (thus a fraction smaller than one is used for the temperature factor). Then, since the pressure is increasing the volume will decrease (thus the pressure factor is a fraction less than one).

V_{2} = (2.6 L) (\frac{273 K}{373 K}) (\frac{700 mm Hg}{760 mm Hg}) = 1.8 L

Exercise

A sample of gas occupies a volume of 425 mL at 15°C and 1.2 atm pressure. Calculate the new pressure, in atm, if the temperature is changed to 25 °C and the volume is changed to 582 mL.

Answer: 0.91 atm

Summary

Boyle showed that the volume of a sample of a gas is inversely proportional to its pressure (Boyle’s law), Charles demonstrated that the volume of a gas is directly proportional to its temperature (in kelvin) at constant pressure (Charles’s law), and Gay-Lussac showed that the pressure of a gas is directly proportional to the temperature (Gay-Lussac’s law).

Key Takeaway

The volume of a gas is inversely proportional to its pressure and directly proportional to its temperature.

Problems

Define gas law. What restrictions are there on the units that can be used for the physical properties?
What unit of temperature must be used for gas laws?
Boyle's law relates the _____________ of a gas inversely with the ___________ of that gas.
Charles's law relates the _____________ of a gas directly with the ___________ of that gas.
What properties must be held constant when applying Boyle's law?
What properties must be held constant when applying Charles's law?
A gas has an initial pressure of 1.445 atm and an initial volume of 1.009 L. What is its new pressure if volume is changed to 0.556 L? Assume temperature and amount are held constant.
A gas has an initial pressure of 633 torr and an initial volume of 87.3 mL. What is its new pressure if volume is changed to 45.0 mL? Assume temperature and amount are held constant.
A gas has an initial pressure of 4.33 atm and an initial volume of 5.88 L. What is its new volume if pressure is changed to 0.506 atm? Assume temperature and amount are held constant.
A gas has an initial pressure of 87.0 torr and an initial volume of 28.5 mL. What is its new volume if pressure is changed to 206 torr? Assume temperature and amount are held constant.
A gas has an initial volume of 638 mL and an initial pressure of 779 torr. What is its final volume in liters if its pressure is changed to 0.335 atm? Assume temperature and amount are held constant.
A gas has an initial volume of 0.966 L and an initial pressure of 3.07 atm. What is its final pressure in torr if its volume is changed to 3450 mL? Assume temperature and amount are held constant.
A gas has an initial volume of 67.5 mL and an initial temperature of 315 K. What is its new volume if temperature is changed to 244 K? Assume pressure and amount are held constant.
A gas has an initial volume of 2.033 L and an initial temperature of 89.3 K. What is its volume if temperature is changed to 184 K? Assume pressure and amount are held constant.
A gas has an initial volume of 655 mL and an initial temperature of 295 K. What is its new temperature if volume is changed to 577 mL? Assume pressure and amount are held constant.
A gas has an initial volume of 14.98 L and an initial temperature of 238 K. What is its new temperature if volume is changed to 12.33 L? Assume pressure and amount are held constant.
A gas has an initial volume of 685 mL and an initial temperature of 29°C. What is its new temperature if volume is changed to 1.006 L? Assume pressure and amount are held constant.
A gas has an initial volume of 3.08 L and an initial temperature of -73°C. What is its new volume if temperature is changed to 104°C? Assume pressure and amount are held constant.

Answers

A gas law is a simple mathematical formula that allows one to predict the physical properties of a gas. The units of changing properties (volume, pressure, etc.) must be the same.
pressure; volume
amount of gas and temperature
2.62 atm
50.3 L
1.95 L
52.3 mL
260 K
444 K, or 171°C