This is "Unit 1", section 1.5 from the book General Chemistry (v. 1.0).
1.5 The Atom
Learning Objective
- To become familiar with the components and structure of the atom.
- To know the relative masses and charges of the subatomic particles-protons, neutrons and electrons
- To be able to tell what the atomic number and the mass number represent in terms of the subatomic particles
- To recognize isotopes of an alement.
- To be able to calculate the atomic weight of an element given the abundance of the isotopes and their masses.
To date, all elements from atomic numbers 1 (hydrogen) to 118 (oganesson) have been discovered or synthesized. The most recent additions (nihonium, moscovium, tennessine, and oganesson) being confirmed by the IUPAC (International Union of Pure and Applied Chemists) on December 30, 2015 and officially named on November 28, 2016. They complete the first seven rows of the periodic table; by definition, each is chemically unique. To understand why they are unique, you need to understand the structure of the atom (the fundamental, individual particle of an element) and the characteristics of its components.
Atoms consist of electronsA subatomic particle with a negative charge that resides around the nucleus of all atoms., protonsA subatomic particle with a positive charge that resides in the nucleus of all atoms., and neutronsA subatomic particle with no charge that resides in the nucleus of almost all atoms..This is an oversimplification that ignores the other subatomic particles that have been discovered, but it is sufficient for our discussion of chemical principles. Some properties of these subatomic particles are summarized in Table 1.5(1) "Properties of Subatomic Particles", which illustrates three important points.
- Electrons and protons have electrical charges that are identical in magnitude but opposite in sign. We usually assign relative charges of -1 and +1 to the electron and proton, respectively.
- Neutrons have approximately the same mass as protons but no charge. They are electrically neutral.
- The mass of a proton or a neutron is about 1836 times greater than the mass of an electron. Protons and neutrons constitute by far the bulk of the mass of atoms.
The discovery of the electron and the proton was crucial to the development of the modern model of the atom and provides an excellent case study in the application of the scientific method. In fact, the elucidation of the atom's structure is one of the greatest detective stories in the history of science.
Table 1.5(1) Properties of Subatomic Particles
| Particle | Mass (g) | Atomic Mass (amu) | Electrical Charge (coulombs) | Relative Charge |
|---|---|---|---|---|
| electron | 9.109 × 10-28 | 0.0005486 | -1.602 נ10-19 | -1 |
| proton | 1.673 נ10-24 | 1.007276 | +1.602 נ10-19 | +1 |
| neutron | 1.675 נ10-24 | 1.008665 | 0 | 0 |
The Electron
Figure 1.5(a) A Gas Discharge Tube Producing Cathode Rays

When a high voltage is applied to a gas contained at low pressure in a gas discharge tube, electricity flows through the gas, and energy is emitted in the form of light. Glow discharge in a low-pressure tube caused by electric current. Performed by Prof. Oliver Zajkov at the Physics Institute at the Ss. Cyril and Methodius University of Skopje, Macedonia. Image Credit: Andrejdam and is licensed under the Creative Commons Attribution-Share Alike 4.0 International license. This is a frame grab from the video.
Long before the end of the 19th century, it was well known that applying a high voltage to a gas contained at low pressure in a sealed tube (called a gas discharge tube) caused electricity to flow through the gas, which then emitted light (Figure 1.5(a) "A Gas Discharge Tube Producing Cathode Rays"). Researchers trying to understand this phenomenon found that an unusual form of energy was also emitted from the cathode, or negatively charged electrode; hence this form of energy was called cathode rays. In 1897, the British physicist J. J. Thomson (1856-1940) proved that atoms were not the ultimate form of matter. He demonstrated that cathode rays could be deflected, or bent, by magnetic or electric fields, which indicated that cathode rays consist of charged particles (Figure 1.5(b) "Deflection of Cathode Rays by an Electric Field"). More important, by measuring the extent of the deflection of the cathode rays in magnetic or electric fields of various strengths, Thomson was able to calculate the mass-to-charge ratio of the particles. These particles were emitted by the negatively charged cathode and repelled by the negative terminal of an electric field. Because like charges repel each other and opposite charges attract, Thomson concluded that the particles had a net negative charge; we now call these particles electrons. Most important for chemistry, Thomson found that the mass-to-charge ratio of cathode rays was independent of the nature of the metal electrodes or the gas, which suggested that electrons were fundamental components of all atoms.
Figure 1.5(b) Deflection of Cathode Rays by an Electric Field

As the cathode rays travel toward the right, they are deflected toward the positive electrode (+), demonstrating that they are negatively charged.
Subsequently, the American scientist Robert Millikan (1868-1953) carried out a series of experiments using electrically charged oil droplets, which allowed him to calculate the charge on a single electron. With this information and Thomson's mass-to-charge ratio, Millikan determined the mass of an electron:
It was at this point that two separate lines of investigation began to converge, both aimed at determining how and why matter emits energy.
Radioactivity
The second line of investigation began in 1896, when the French physicist Henri Becquerel (1852-1908) discovered that certain minerals, such as uranium salts, emitted a new form of energy. Becquerel's work was greatly extended by Marie Curie (1867-1934) and her husband, Pierre (1854-1906); all three shared the Nobel Prize in Physics in 1903. Marie Curie coined the term radioactivityThe spontaneous emission of energy rays (radiation) by matter. (from the Latin radius, meaning "ray") to describe the emission of energy rays by matter. She found that one particular uranium ore, pitchblende, was substantially more radioactive than most, which suggested that it contained one or more highly radioactive impurities. Starting with several tons of pitchblende, the Curies isolated two new radioactive elements after months of work: polonium, which was named for Marie's native Poland, and radium, which was named for its intense radioactivity. Pierre Curie carried a vial of radium in his coat pocket to demonstrate its greenish glow, a habit that caused him to become ill from radiation poisoning well before he was run over by a horse-drawn wagon and killed instantly in 1906. Marie Curie, in turn, died of what was almost certainly radiation poisoning.

Radium bromide illuminated by its own radioactive glow. This 1922 photo was taken in the dark in the Curie laboratory.
Building on the Curies' work, the British physicist Ernest Rutherford (1871-1937) performed decisive experiments that led to the modern view of the structure of the atom. While working in Thomson's laboratory shortly after Thomson discovered the electron, Rutherford showed that compounds of uranium and other elements emitted at least two distinct types of radiation. One was readily absorbed by matter and seemed to consist of particles that had a positive charge and were massive compared to electrons. Because it was the first kind of radiation to be discovered, Rutherford called these substances α particles. Rutherford also showed that the particles in the second type of radiation, β particles, had the same charge and mass-to-charge ratio as Thomson's electrons; they are now known to be high-speed electrons. A third type of radiation, γ rays, was discovered somewhat later and found to be similar to a lower-energy form of radiation called x-rays, now used to produce images of bones and teeth.
These three kinds of radiation- α particles, β particles, and γ rays-are readily distinguished by the way they are deflected by an electric field and by the degree to which they penetrate matter. As Figure 1.5(c) "Effect of an Electric Field on α Particles, β Particles, and γ Rays" illustrates, α particles and β particles are deflected in opposite directions; α particles are deflected to a much lesser extent because of their higher mass-to-charge ratio. In contrast, γ rays have no charge, so they are not deflected by electric or magnetic fields. Figure 1.5(d) "Relative Penetrating Power of the Three Types of Radiation" shows that α particles have the least penetrating power and are stopped by a sheet of paper, whereas β particles can pass through thin sheets of metal but are absorbed by lead foil or even thick glass. In contrast, γ-rays can readily penetrate matter; thick blocks of lead or concrete are needed to stop them.
Figure 1.5(c) Effect of an Electric Field on α Particles, β Particles, and γ Rays

A negative electrode deflects negatively charged β particles, whereas a positive electrode deflects positively charged α particles. Uncharged γ rays are unaffected by an electric field. (Relative deflections are not shown to scale.)
Figure 1.5(d) Relative Penetrating Power of the Three Types of Radiation

A sheet of paper stops comparatively massive α particles, whereas β particles easily penetrate paper but are stopped by a thin piece of lead foil. Uncharged γ rays penetrate the paper and lead foil; a much thicker piece of lead or concrete is needed to absorb them.
The Atomic Model
Once scientists concluded that all matter contains negatively charged electrons, it became clear that atoms, which are electrically neutral, must also contain positive charges to balance the negative ones. Thomson proposed that the electrons were embedded in a uniform sphere that contained both the positive charge and most of the mass of the atom, much like raisins in plum pudding or chocolate chips in a cookie (Figure 1.5(e) "Thomson's Plum Pudding or Chocolate Chip Cookie Model of the Atom").
Figure 1.5(e) Thomson's Plum Pudding or Chocolate Chip Cookie Model of the Atom

In this model, the electrons are embedded in a uniform sphere of positive charge.
In a single famous experiment, however, Rutherford showed unambiguously that Thomson's model of the atom was impossible. Rutherford aimed a stream of α particles at a very thin gold foil target (part (a) in Figure 1.5(f) "A Summary of Rutherford's Experiments") and examined how the α particles were scattered by the foil. Gold was chosen because it could be easily hammered into extremely thin sheets with a thickness that minimized the number of atoms in the target. If Thomson's model of the atom were correct, the positively charged α particles should crash through the uniformly distributed mass of the gold target like cannonballs through the side of a wooden house. They might be moving a little slower when they emerged, but they should pass essentially straight through the target (part (b) in Figure 1.5(f) "A Summary of Rutherford's Experiments"). To Rutherford's amazement, a small fraction of the α particles were deflected at large angles, and some were reflected directly back at the source (part (c) in Figure 1.5(f) "A Summary of Rutherford's Experiments"). According to Rutherford, "It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."
Figure 1.5(f) A Summary of Rutherford's Experiments

(a) A representation of the apparatus Rutherford used to detect deflections in a stream of α particles aimed at a thin gold foil target. The particles were produced by a sample of radium. (b) If Thomson's model of the atom were correct, the α particles should have passed straight through the gold foil. (c) But a small number of α particles were deflected in various directions, including right back at the source. This could be true only if the positive charge were much more massive than the α particle. It suggested that the mass of the gold atom is concentrated in a very small region of space, which he called the nucleus.
Rutherford's results were not consistent with a model in which the mass and positive charge are distributed uniformly throughout the volume of an atom. Instead, they strongly suggested that both the mass and positive charge are concentrated in a tiny fraction of the volume of an atom, which Rutherford called the nucleusThe central core of an atom where protons and any neutrons reside.. It made sense that a small fraction of the α particles collided with the dense, positively charged nuclei in either a glancing fashion, resulting in large deflections, or almost head-on, causing them to be reflected straight back at the source.
Although Rutherford could not explain why repulsions between the positive charges in nuclei that contained more than one positive charge did not cause the nucleus to disintegrate, he reasoned that repulsions between negatively charged electrons would cause the electrons to be uniformly distributed throughout the atom's volume.Today we know that strong nuclear forces, which are much stronger than electrostatic interactions, hold the protons and the neutrons together in the nucleus. For this and other insights, Rutherford was awarded the Nobel Prize in Chemistry in 1908. Unfortunately, Rutherford would have preferred to receive the Nobel Prize in Physics because he thought that physics was superior to chemistry. In his opinion, "All science is either physics or stamp collecting." (The authors of this text do not share Rutherford's view!)
Subsequently, Rutherford established that the nucleus of the hydrogen atom was a positively charged particle, for which he coined the name proton in 1920. He also suggested that the nuclei of elements other than hydrogen must contain electrically neutral particles with approximately the same mass as the proton. The neutron, however, was not discovered until 1932, when James Chadwick (1891-1974, a student of Rutherford; Nobel Prize in Physics, 1935) discovered it. As a result of Rutherford's work, it became clear that an α particle contains two protons and two neutrons and is therefore simply the nucleus of a helium atom.
The historical development of the different models of the atom's structure is summarized in Figure 1.5(g) "A Summary of the Historical Development of Models of the Components and Structure of the Atom". Rutherford's model of the atom is essentially the same as the modern one, except that we now know that electrons are not uniformly distributed throughout an atom's volume. Instead, they are distributed according to a set of principles described in Chapter 3 of this textbook. Figure 1.5(h) "The Evolution of Atomic Theory, as Illustrated by Models of the Oxygen Atom" shows how the model of the atom has evolved over time from the indivisible unit of Dalton to the modern view taught today.
Figure 1.5(g) A Summary of the Historical Development of Models of the Components and Structure of the Atom

The dates in parentheses are the years in which the key experiments were performed.
Figure 1.5(h) The Evolution of Atomic Theory, as Illustrated by Models of the Oxygen Atom

Rutherford's nuclear model of the atom helped explain why atoms of different elements exhibit different chemical behavior. The identity of an element is defined by its atomic number (Z)The number of protons in the nucleus of an atom of an element., the number of protons in the nucleus of an atom of the element. The atomic number is therefore different for each element. The known elements are arranged in order of increasing Z in the periodic tableA chart of the chemical elements arranged in rows of increasing atomic number so that the elements in each column (group) have similar chemical properties.. The chemistry of each element is determined by its number of protons and electrons. In a neutral atom, the number of electrons equals the number of protons.
Unlike protons, the number of neutrons is not absolutely fixed for most elements. Atoms that have the same number of protons, and hence the same atomic number, but different numbers of neutrons are called isotopesAtoms that have the same numbers of protons but different numbers of neutrons.. All isotopes of an element have the same number of protons and electrons, which means they exhibit the same chemistry. The isotopes of an element differ only in their atomic mass, which is given by the mass number (A)The number of protons and neutrons in the nucleus of an atom of an element., the sum of the numbers of protons and neutrons.
The element carbon (C) has an atomic number of 6, which means that all neutral carbon atoms contain 6 protons and 6 electrons. In a typical sample of carbon-containing material, 98.89% of the carbon atoms also contain 6 neutrons, so each has a mass number of 12. An isotope of any element can be uniquely represented as where X is the atomic symbol of the element, A is the mass number and Z is the atomic number. The isotope of carbon that has 6 neutrons is therefore The subscript indicating the atomic number is actually redundant because the atomic symbol already uniquely specifies Z. Consequently, is more often written as 12C, which is read as 'carbon-12.'
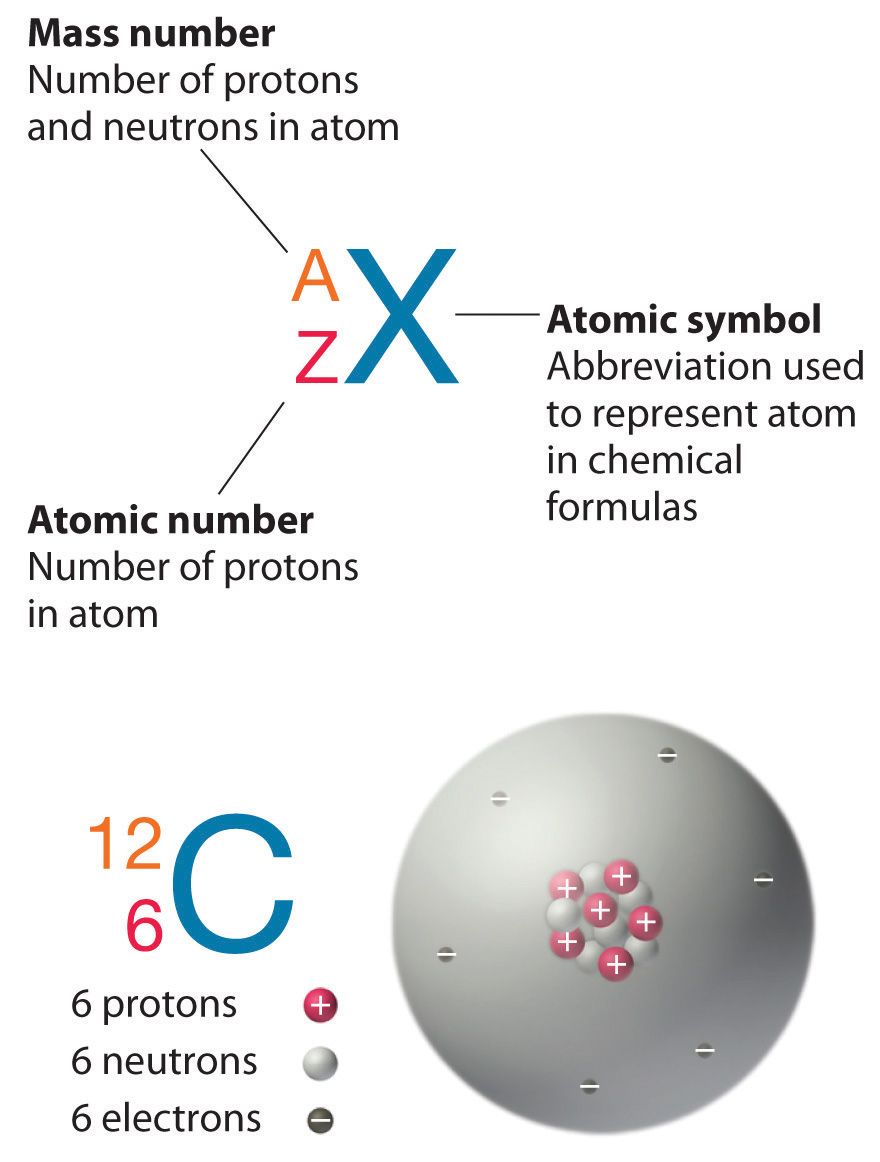
In addition to 12C, a typical sample of carbon contains 1.11% (13C), with 7 neutrons and 6 protons, and a trace of (14C), with 8 neutrons and 6 protons. The nucleus of 14C is not stable, however, but undergoes a slow radioactive decay that is the basis of the carbon-14 dating technique used in archaeology. Many elements other than carbon have more than one stable isotope; tin, for example, has 10 isotopes. The properties of some common isotopes are in Table 1.5(2) "Properties of Selected Isotopes".
Table 1.5(2) Properties of Selected Isotopes
| Element | Symbol | Atomic Mass (amu) | Isotope Mass Number | Isotope Masses (amu) | Percent Abundances (%) |
|---|---|---|---|---|---|
| hydrogen | H | 1.0079 | 1 | 1.007825 | 99.9855 |
| 2 | 2.014102 | 0.0115 | |||
| boron | B | 10.81 | 10 | 10.012937 | 19.91 |
| 11 | 11.009305 | 80.09 | |||
| carbon | C | 12.011 | 12 | 12 (defined) | 99.89 |
| 13 | 13.003355 | 1.11 | |||
| oxygen | O | 15.9994 | 16 | 15.994915 | 99.757 |
| 17 | 16.999132 | 0.0378 | |||
| 18 | 17.999161 | 0.205 | |||
| iron | Fe | 55.845 | 54 | 53.939611 | 5.82 |
| 56 | 55.934938 | 91.66 | |||
| 57 | 56.935394 | 2.19 | |||
| 58 | 57.933276 | 0.33 | |||
| uranium | U | 238.03 | 234 | 234.040952 | 0.0054 |
| 235 | 235.043930 | 0.7204 | |||
| 238 | 238.050788 | 99.274 |
Sources of isotope data: G. Audi et al., Nuclear Physics A 729 (2003): 337-676; J. C. Kotz and K. F. Purcell, Chemistry and Chemical Reactivity, 2nd ed., 1991.
Example 1.5-1
An element with three stable isotopes has 82 protons. The separate isotopes contain 124, 125, and 126 neutrons. Identify the element and write symbols for the isotopes.
Given: number of protons and neutrons
Asked for: element and atomic symbol
Strategy:
Step 1 Refer to the periodic table and use the number of protons to identify the element.
Step 2 Calculate the mass number of each isotope by adding together the numbers of protons and neutrons.
Step 3 Give the symbol of each isotope with the mass number as the superscript and the number of protons as the subscript, both written to the left of the symbol of the element.
Solution:
Step 1 The element with 82 protons (atomic number of 82) is lead: Pb.
Although the masses of the electron, the proton, and the neutron are known to a high degree of precision (Table 1.5(1) "Properties of Subatomic Particles"), the mass of any given atom is not simply the sum of the masses of its electrons, protons, and neutrons. For example, the ratio of the masses of 1H (hydrogen) and 2H (deuterium) is actually 0.500384, rather than 0.49979 as predicted from the numbers of neutrons and protons present. Although the difference in mass is small, it is extremely important because it is the source of the huge amounts of energy released in nuclear reactions.
Because atoms are much too small to measure individually and do not have a charge, there is no convenient way to accurately measure absolute atomic masses. Scientists can measure relative atomic masses very accurately, however, using an instrument called a mass spectrometer. The technique is conceptually similar to the one Thomson used to determine the mass-to-charge ratio of the electron. First, electrons are removed from or added to atoms or molecules, thus producing charged particles called ionsA charged particle produced when one or more electrons is removed from or added to an atom or molecule.. When an electric field is applied, the ions are accelerated into a separate chamber where they are deflected from their initial trajectory by a magnetic field, like the electrons in Thomson's experiment. The extent of the deflection depends on the mass-to-charge ratio of the ion. By measuring the relative deflection of ions that have the same charge, scientists can determine their relative masses (Figure 1.5(i) "Determining Relative Atomic Masses Using a Mass Spectrometer"). Thus it is not possible to calculate absolute atomic masses accurately by simply adding together the masses of the electrons, the protons, and the neutrons, and absolute atomic masses cannot be measured, but relative masses can be measured very accurately. It is actually rather common in chemistry to encounter a quantity whose magnitude can be measured only relative to some other quantity, rather than absolutely. We will encounter many other examples later in this text. In such cases, chemists usually define a standard by arbitrarily assigning a numerical value to one of the quantities, which allows them to calculate numerical values for the rest.
Step 2 For the first isotope, A = 82 protons + 124 neutrons = 206. Similarly A = 82 + 125 = 207 and A = 82 + 126 = 208 for the second and third isotopes, respectively.
Step 3 Their symbols are thus
, and
which are usually abbreviated as
206Pb, 207Pb and 208Pb
Exercise: Identify the element that contains 35 protons, and write the symbols for its isotopes with 44 and 46 neutrons.
Answer: and or, more commonly 79Br and 81Br.
Figure 1.5(i) Determining Relative Atomic Masses Using a Mass Spectrometer

Chlorine consists of two isotopes, 35Cl and 37Cl, in approximately a 3:1 ratio. (a) When a sample of elemental chlorine is injected into the mass spectrometer, electrical energy is used to dissociate the Cl2 molecules into chlorine atoms and convert the chlorine atoms to Cl+ ions. The ions are then accelerated into a magnetic field. The extent to which the ions are deflected by the magnetic field depends on their relative mass-to-charge ratios. Note that the lighter 35Cl+ ions are deflected more than the heavier 37Cl+ ions. By measuring the relative deflections of the ions, chemists can determine their mass-to-charge ratios and thus their masses. (b) Each peak in the mass spectrum corresponds to an ion with a particular mass-to-charge ratio. The abundance of the two isotopes can be determined from the heights of the peaks.
The arbitrary standard that has been established for describing atomic mass is the atomic mass unit (amu)One-twelfth of the mass of one atom of C 12 ; 1 amu = 1 . 66 × 1 0 − 24 g ., defined as one-twelfth of the mass of one atom of 12C. Because the masses of all other atoms are calculated relative to the 12C standard, 12C is the only atom listed in Table 1.5(2) "Properties of Selected Isotopes" whose exact atomic mass is equal to the mass number. Experiments have shown that 1 amu = 1.66 נ10-24 g.
Mass spectrometric experiments give a value of 0.167842 for the ratio of the mass of 2H to the mass of 12C, so the absolute mass of 2H is
The masses of the other elements are determined in a similar way.
The periodic table lists the atomic masses of all the elements. If you compare these values with those given for some of the isotopes in Table 1.5(2) "Properties of Selected Isotopes", you can see that the atomic masses given in the periodic table never correspond exactly to those of any of the isotopes. Because most elements exist as mixtures of several stable isotopes, the atomic mass of an element is defined as the weighted average of the masses of the isotopes. For example, naturally occurring carbon is largely a mixture of two isotopes: 98.89% 12C (mass = 12 amu by definition) and 1.11% 13C (mass = 13.003355 amu). The percent abundance of 14C is so low that it can be ignored in this calculation. The average atomic mass of carbon is then calculated as
(O.9889 × 12 amu) + (0.00111 × 13.003344 amu) = 12.01 amuCarbon is predominantly 12C, so its average atomic mass should be close to 12 amu, which is in agreement with our calculation.
The value of 12.01 is shown under the symbol for C in the periodic table, although without the abbreviation amu, which is customarily omitted. Thus the tabulated atomic mass of carbon or any other element is the weighted average of the masses of the naturally occurring isotopes.
Example 1.5-2
Naturally occurring bromine consists of the two isotopes listed in the following table:
| Isotope | Exact Mass (amu) | Percent Abundance (%) |
|---|---|---|
| 79Br | 78.9183 | 50.69 |
| 81Br | 80.9163 | 49.31 |
Calculate the atomic mass of bromine.
Given: exact mass and percent abundance
Asked for: atomic mass
Strategy:
Step 1 Convert the percent abundances to decimal form to obtain the mass fraction of each isotope.
Step 2 Multiply the exact mass of each isotope by its corresponding mass fraction (percent abundance divided by 100) to obtain its weighted mass.
Step 3 Add together the weighted masses to obtain the atomic mass of the element.
Step 4 Check to make sure that your answer makes sense.
Solution:
Step 1 The atomic mass is the weighted average of the masses of the isotopes. In general, we can write
atomic mass of element = [(mass of isotope 1 in amu) (mass fraction of isotope 1)] + [(mass of isotope 2) (mass fraction of isotope 2)] + . . .Bromine has only two isotopes. Converting the percent abundances to mass fractions gives
79Br: and 81Br:
Step 2 Multiplying the exact mass of each isotope by the corresponding mass fraction gives the isotope's weighted mass:
79Br: (79.9183 amu)(0.5069) = 40.00 amu
81Br: (80.9163 amu)(0.4931) = 39.90 amu
Step 3 The sum of the weighted masses is the atomic mass of bromine:
40.00 amu + 39.90 amu = 79.90 amu
Step 4 This value is about halfway between the masses of the two isotopes, as expected because the percent abundance of each is approximately 50%.
Exercise
Magnesium has the three isotopes listed in the following table:
| Isotope | Exact Mass (amu) | Percent Abundance (%) |
|---|---|---|
| 24Mg | 23.98504 | 78.70 |
| 25Mg | 24.98584 | 10.13 |
| 26Mg | 25.98259 | 11.17 |
Use these data to calculate the atomic mass of magnesium.
Answer: 24.31 amu
Summary
Atoms, the smallest particles of an element that exhibit the properties of that element, consist of negatively charged electrons around a central nucleus composed of more massive positively charged protons and electrically neutral neutrons. Radioactivity is the emission of energetic particles and rays (radiation) by some substances. Three important kinds of radiation are α particles (helium nuclei), β particles (electrons traveling at high speed), and γ rays (similar to x-rays but higher in energy).
Each atom of an element contains the same number of protons, which is the atomic number (Z). Neutral atoms have the same number of electrons and protons. Atoms of an element that contain different numbers of neutrons are called isotopes. Each isotope of a given element has the same atomic number but a different mass number (A), which is the sum of the numbers of protons and neutrons. The relative masses of atoms are reported using the atomic mass unit (amu), which is defined as one-twelfth of the mass of one atom of carbon-12, with 6 protons, 6 neutrons, and 6 electrons. The atomic mass of an element is the weighted average of the masses of the naturally occurring isotopes. When one or more electrons are added to or removed from an atom or molecule, a charged particle called an ion is produced, whose charge is indicated by a superscript after the symbol.
Key Takeaways
- The atom consists of discrete particles that govern its chemical and physical behavior.
- The mass of an atom is a weighted average that is largely determined by the number of its protons and neutrons, whereas the number of protons and electrons determines its charge.





